| Вычерчивание профиля зубца |
 |
|
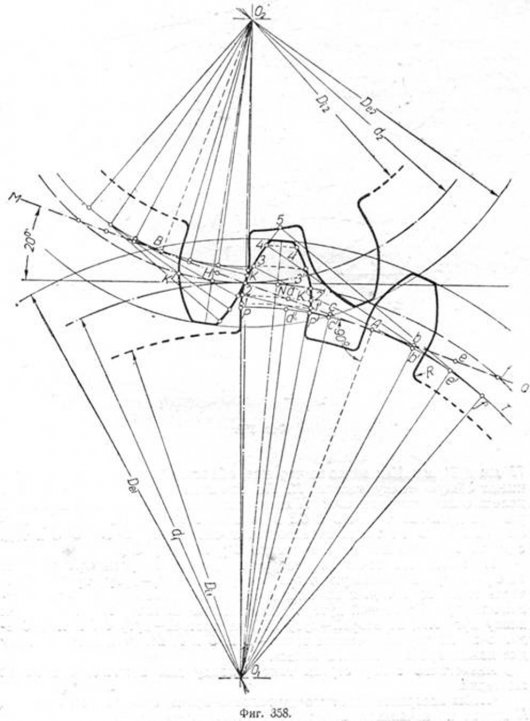
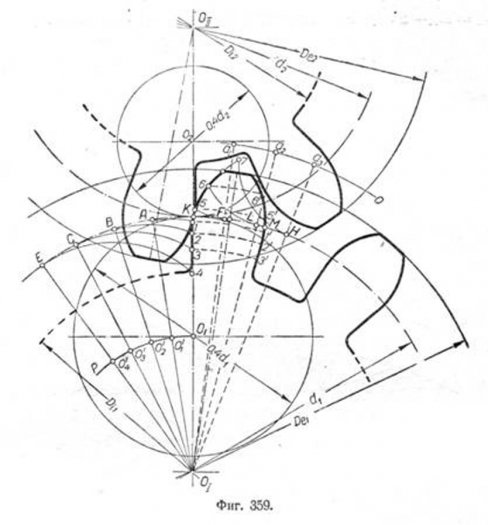
Эвольвентный профиль зубца. Построение эвольвенты в общем виде было рассмотрено в главе „Геометрическое черчение". Рассмотрим практическое применение этой кривой при вычерчивании профиля зубцов зубчатых колёс. Пусть даны два цилиндрических зубчатых колеса с модулем m=18 и числом зубцов: первого z1 = 18, второго z2 = 12. Для вычерчивания профиля зубцов пользуемся ранее приведёнными формулами. Находим размеры элементов зубцов. Первое колесо: d1 = m • z1 = 18 • 18 = 324 мм; De1 = m (z1 + 2) = 18(18 + 2) = 360 мм; Di1= De1 — 2 • 2,2 m = 360 — 2 • 2,2 • 18 = 280,8 мм; t= ? • m = 3,14 • 18 = 56,52 мм. Второе колесо: d2 = m • z2 = 18 • 12 = 216 мм; De2 = m (z2 + 2) = 18 (12 + 2) = 252 мм; Di2 = De2 — 2 • 2,2 m = 252 — 2 • 2,2 • 18 = 172,8 мм. Проводим из центров O1 и 02 (фиг. 358) начальные окружности, окружности выступов и окружности впадин, обращая при этом внимание на то, чтобы начальные окружности обоих колёс имели одну общую точку касания К, лежащую на линии центров O1—O2. Далее через точку К проводим под углом 20° к общей касательной начальных окружностей прямую MQ и, опустив из центров О1 и 02 на эту прямую перпендикуляры, получим точки А и В. Из центра О1 радиусом О1А описываем основную окружность (на чертеже показана только часть её). Делим прямую KA на равное число частей, например на три, и отметим точки деления буквами d, с и вправо от точки А —b, e, f. Затем откладываем от точки А влево и вправо эти отрезки по дуге основной окружности PAT; точки деления обозначаем буквами d', с', b', е'у f ' и соединяем их радиусами с центром О1. Проводим через точки d', c', b', e', f' перпендикулярно к радиусам лучи. Далее на этих лучах откладываем отрезки: на луче d'—отрезок AC, получим точку 1; на луче с'—отрезок Ad, получим точку 2 и т. д. Соединив по лекалу найденные таким образом точки 1, 2, 3, 4, 5, получим эвольвенту, по которой должен быть вычерчен профиль зубца большего колеса. Аналогичным построением получим профиль зубца и для второго колеса. Чтобы вычертить полный профиль зубца, откладываем по дугам начальных окружностей от точки К вправо и влево размер толщины зубца s = KK'. Делим s пополам и через середины зубцов, отмеченные точками N и H, проводим прямые O1N и 02H, а затем из центра 01 описываем ряд дуг: 1-1'; 2—2'; 3—3' и т. д. Эти дуги делятся прямой 01N пополам. Проводя таким образом дуги из центра 02, легко построим полный профиль зубца и для второго колеса. Следует заметить, что по эвольвенте вычерчивается часть зубца—кривая PK5, которая начинается от точки Я, лежащей на основной окружности. Нижняя часть зубца вычерчивается по прямой, имеющей направление от точки P к центру O1. Место примыкания ножки зубца к окружности впадин скругляется радиусом R = 0,2 m. В нашем примере R = 3,6 мм. Циклоидальный профиль зубца. Образование профиля зубца колеса производится по кривым—эпициклоиде и гипоциклоиде. Пусть дано: модуль m = 16, число зубцов первого колеса z1 = 12, второго — z2 = 8. Для построения зубцов цилиндрических колёс определим сначала их конструктивные элементы. Диаметры начальных окружностей d1 = m • z1 = 192 мм; d2 = m• z2 = 128 мм. Диаметры окружностей выступов De1 = m (z1+ 2) = 224 мм; De2 = m (z2 + 2) == 160 мм. Диаметры окружностей впадин Di1=De1- 2*2,2 m = 153,6 мм; Di2=De2—2.2,2 m = 89,6 мм. Шаг зацепления t = ?* m = 50,24 мм. Толщина зубца s = 0,487 *t = 24,47 мм, 77 мм и 51 мм. Как видно из чертежа, обе вспомогательные окружности имеют общую точку касания К. По начальной окружности большого колеса откладываем от точки К влево равные по величине произвольного размера дуги KA, AB, ВС и СЕ и из центра 0I радиусом 0I —О1 описываем дугу ОI Р. Точки пересечения лучей 0IA, ОIВ, 0IС и т.д. с дугой О1Р отмечаем соответственно 0'1 0'2, 0'3, 0'4. Принимая эти точки за центры, проводим радиусом О1К ряд дуг: из O1'—дугу, проходящую через точку Л, из 0'2 - дугу, проходящую через точку В, и т. д. и на этих дугах откладываем длины соответствующих дуг. На первой дуге, проходящей через точку A, откладываем длину дуги AK, на второй—дугу BK, на третьей—дугу CK и т. д. Соединив по лекалу полученные точки—1, 2, 3 и 4, получим гипоциклоиду для ножки зубца большого колеса. Аналогично этому строим гипоциклоиду для ножки зубца малой шестерни. Чтобы построить эпициклоиду головки зубца, откладываем от точки К вправо по начальной окружности этого колеса несколько равных по величине произвольного размера дуг KF, FL, LH и проводим из центра OI радиусом 0I—02 дугу 02Q. Пересечения лучей 0I, F, 01 L u OIH дадут на проведённой дуге точки a1, а2 и а3. Принимая эти точки за центры, проводим радиусом O2K из точки а1 дугу, проходящую через точку F. из а2—дугу через L и т.д. Отложив затем на первой дуге длину дуги FK, получим точку 5, на второй дуге—длину дуги LK, получим точку 6 и т. д. Соединив точки К, 5, 6 и 7 по лекалу до пересечения с окружностью выступов большего колеса, получим эпициклоиду головки. Чтобы построить полный профиль этого зубца, необходимо по начальной окружности большего колеса отложить толщину зубца s = 24 мм, равную КМ, разделить её пополам (на чертеже середина отмечена штрих-пунктирной линией, выходящей из OI ) и затем симметрично построить, справа от этой линии, точки 3', 2', 1', 5', 6' и т. д. Построение профиля головки зубца малого колеса производится аналогично построению зубца большего. Для вычерчивания остальных зубцов следует разделить начальные окружности на равное число частей, соответственно числу зубцов шестерни. Расстояние между центрами каждых двух смежных зубцов по дуге начальной окружности должно равняться шагу зацепления t. Упрощённый способ вычерчивания профиля зубца. Этот способ применяется для вычерчивания эвольвентного профиля зубцов зубчатых колёс с литыми зубцами, а также для указания обработки, размеров элементов зубца на рабочем чертеже зубчатого колеса и т. п. Рассмотрим это построение на примере.
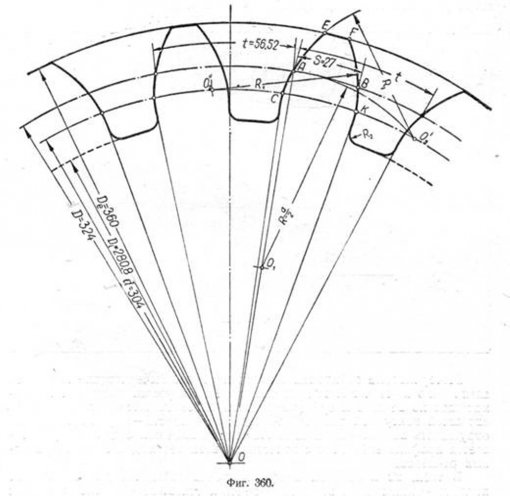
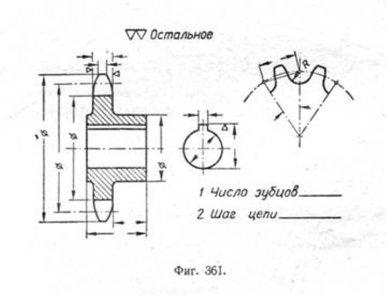
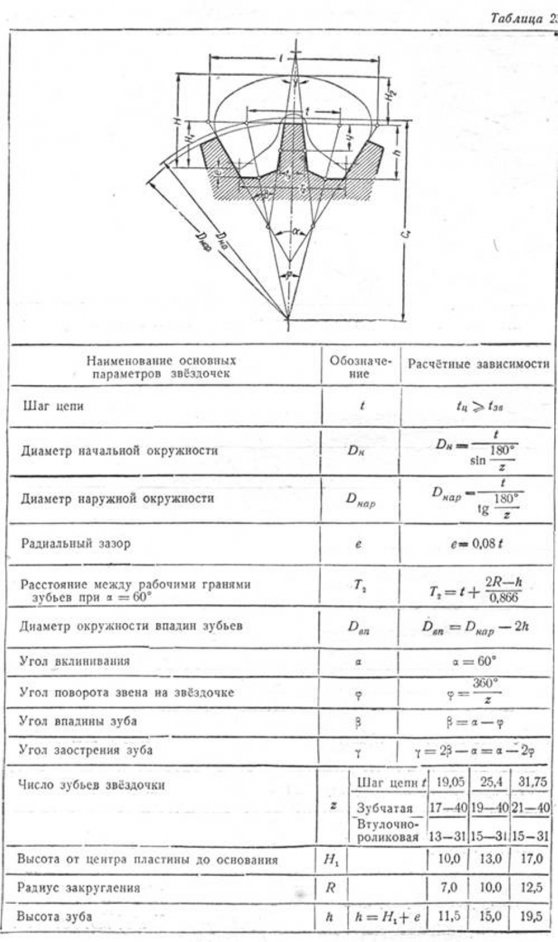
точки радиусом R1 проводим дугу CAE, Сделав из точки В на основной окружности засечку тем же радиусом R1 получим точку 02", из которой описываем дугу ВК. Точки САЕFВК принадлежат очертанию головки зубца. Ножка зубца строится по прямым линиям, имеющим направление от точек А и В к центру О. Сопряжение линий профиля ножки с окружностью впадин выполняется радиусом R2, равным 0,2 m. Профиль остальных зубцов строится аналогичным способом. Откладываем по начальной окружности шаг t и толщину зубца s, затем радиусом R1 строим головку зубца и т. д. Вычерчивание звёздочек цепных передач. Вычерчивание звёздочек аналогично вычерчиванию зубчатых колёс. Наружная окружность, проходящая по вершинам зубьев звёздочки, вычерчивается на главном виде сплошной контурной линией, начальная окружность-штрих-пунктирной, окружность впадин—штриховой. На том же виде или отдельно вычерчивается профиль звёздочки с нанесением всех необходимых конструктивных размеров. В табл. 22 приведены профили зубьев звёздочек для приводных втулочно-роликовых и втулочных цепей и основные зависимости для их построения. В табл. 23 приведены данные для звёздочек зубчатых цепей. На фиг. 361 дан конструктивный чертёж звёздочки для втулочно-роликовой цепи. |