Техническое черчение

Представление о цилиндрической резьбе можно составить из следующего.

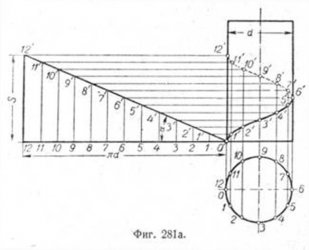
Пусть дан круговой цилиндр диаметром d и гибкий прямоугольный треугольник, у которого горизонтальный катет равен ?d, а вертикальный S=?dtga (фиг. 281а). Если треугольник навивать на боковую поверхность цилиндра, то гипотенуза сделает вокруг цилиндра один оборот и образует винтовую ли­нию, обозначенную точ­ками 0', 1', 2'... 12'. Угол между гипотенузой и го­ризонтальным катетом на­зывают углом подъёма винтовой линии, а высоту S=?dtg a—шагом винто­вой линии.

Если вдоль винтовой линии перемещать пло­скую фигуру в виде тре­угольника, прямоуголь­ника или трапеции так, чтобы одна из точек при перемещении фигуры на­ходилась на винтовой линии, а плоскость фи­гуры проходила через ось цилиндра и сохра­няла постоянные углы наклона к винтовой линии и к оси цилиндра, то образуется виток, профиль которого будет соответствовать профилю плоской фигуры. Такая нитка (виток) носит название резьбового витка. Резьбы бывают однозаходные и многозаходные. Определить число за­ходов можно по торцу резьбового изделия. Число заходов резьбы соот­ветствует числу ниток, выходящих на торец винта.

Представление о многозаходных винтовых линиях легко составить из следующего.

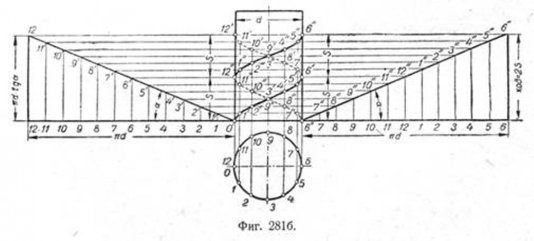
Пусть дан круговой цилиндр диаметра d и два одинаковых гибких прямоугольных треугольника, у которых большой катет равен ?d, а другой—?dtga (фиг. 2816), причём вершины треугольников при углах a расположены в диаметрально противоположных точках 0—6. Если начнём навивать треугольники на боковую поверхность цилиндра (в нашем при мере против часовой стрелки), то на ней образуются соответственно две винтовые линии: 0', 1', 2'... 12' и 6", 7"... 12'', 1"... 6'' т. е. два захода.

Заметим, что концы винтовых линий расположились так же диаметрально противоположно, как и их начала. Отсюда следует, что при се­чении цилиндра любой плоскостью, перпендикулярной к его оси, точки винтовых линий, лежащие в плоскости сечения, всегда (при двух заходах) будут находиться диаметрально противоположно. Заметим также, что в этом примере на высоте хода, равном ?dtga, получилось два витка. Следо­вательно, одному ходу соответствует два шага, т. е. 2S. В предыдущем примере при одном заходе ход был равен шагу S. При трёхзаходной резьбе одному ходу будет соответствовать три шага—35 и т. д.

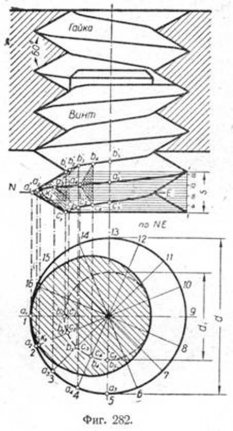Построение однозаходного винта с резьбой треугольного профиля. Пусть требуется построить винтовую поверхность для винта со спе­циальной метрической резьбой, имею­щей наружный диаметр резьбы d, внутренний—d₁ и шаг S (фиг. 282). Построение выполняется следующим образом. Строим в плане окружности диаметров d и d₁ а на вертикальной проекции, соответственно шагу S,- профиль резьбы. Делим окружность диаметра d на чётное число равных частей, например на 16. На такое же число частей делим и шаг S. Верти­кальная проекция профиля a'₁b'₁c'₁ спроектируется в натуральную вели­чину, а горизонтальная изобразится в виде отрезка а₁b₁c₁ совпадающего с горизонтальной осью 1—9.

Чтобы построить винтовую нитку, перемещаем профиль резьбы от одного положения к другому так, чтобы осно­вание треугольника профиля резьбы скользило по внутреннему диаметру d₁ а плоскость его в любой момент проходила через ось винта.

Пусть профиль резьбы ABC зай­мёт положение a₄b₄c₄ на линии деле­ния 4—12. Вертикальные проекции этих точек должны быть на соответ­ствующих линиях деления.

Так, например, точка с₄' будет находиться на четвёртой горизонталь­ной линии.

Точку b'₄ легко найти из равенства c'₁b'₁=c'₄b'₄. Точка a'₄ спроектируется на 12-ю горизонтальную прямую.

Перемещая профиль резьбы дальше, получим на соответствую­щих горизонтальных прямых ряд точек, которые будут принадлежать искомой нитке.

Если винт разрезать секущей плоскостью NE, параллельной гори­зонтальной плоскости проекций, то сечение винта примет вид, показан­ный на плане.

Чтобы уяснить построение точек, принадлежащих контуру сечения, достаточно определить проекции нескольких точек. Пусть плоскость треугольника ABC расположится параллельно вертикальной плоскости, тогда проекции треугольника сoответственно будут a'₁b'₁c'₁ и а₁b₁c_1i. Се­кущая плоскость NE пройдёт через точку А. Проекции этой точки а₁ и a'₁ строятся легко.

В новом положении треугольника, отмеченном проекциями a₂b₂с₂ и a'₂b'₂c'₂, секущая плоскость NE уже не пересечёт вершины треуголь­ника в точке А, а пройдёт несколько ниже и встретит прямую АС в точке К. Проекции её соответственно будут к₂ и k'₂. Как видно, точка К₂ приблизилась к внутреннему диаметру винта и отошла от точки А. Таким образом можно определить и остальные точки контура сечения.

Построение винтовой поверхности однозаходного винта с прямо­угольной резьбой по наружному диаметру d, внутреннему d₁ и шагу S (фиг. 283). Строим в плане окружности диаметров d и d₁. Делим боль­шую окружность на 16 равных частей. На вертикальной проекции, со­ответственно шагу S, строим очертание профиля резьбы. Затем делим шаг S на 16 равных частей и через точки деления проводим горизон­тальные прямые.

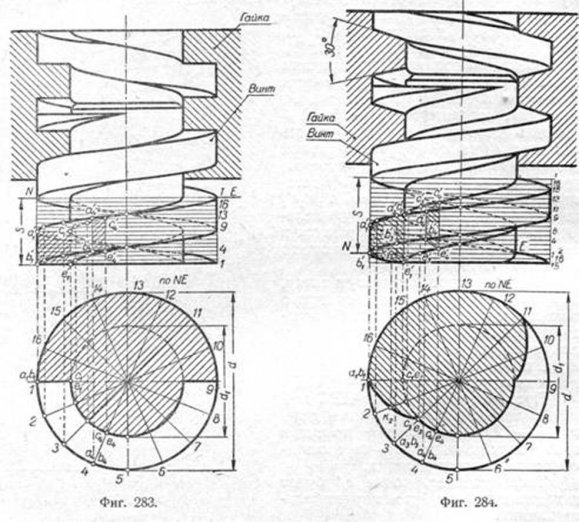
Перемещаем профиль резьбы от одного положения к другому так, как это было разъяснено в предыдущем примере. Начальное положение профиля соответствует на горизонтальной проекции а₁с₁е₁b₁, на вертикальной—а'₁с'₁е'₁b'₁. Если профиль расположится на линии деления 4—12, то на горизонтальной проекции он займёт положение соответственно а₄с₄е₄b₄. Чтобы определить вертикальную проекцию квадрата сечения профиля резьбы, проектируем точки b₄ и е₄ на четвёртую линию деления—b'₄ и е'₄, а а₄ и c₄—на двенадцатую линию; получим точки а'₄ и c'₄. При этом a'₄b'₄ = c'₄e'₄ = a'₁b'₁ = c'₁e'₁. Как видно, проекция квадрата изобразилась в виде прямоугольника. Если квадрат расположится по ли­нии деления 5—73, то на вертикальной проекции он изобразится в виде прямой, совпадающей с осью винта. Производя таким образом построе­ние точек и дальше, получим винтовую поверхность однозаходного винта. Если винт разрезать поперёк секущей плоскостью NE, то сечение при­мет вид, показанный на плане. Если бы секущая плоскость NE была проведена выше или ниже на полшага, то сечение повернулось бы на 180°.

Построение винтовой поверхности винта с трапецоидальной резьбой наружного диаметра d, внутреннего d₁ и шага S (фиг.284).Чтобы выполнить построение, нужно разделить окружность большого диаметра на 16 равных частей. На такое же число нужно разделить и шаг резьбы. Профиль резь­бы представляет равнобокую трапецию, вертикальная проекция которой a'₁b'₁e'₁c'₁. Чтобы построить винтовую поверхность этой резьбы, пере­мещаем вокруг оси винта профиль резьбы так, чтобы большая сторона трапеции скользила по внутреннему диаметру d₁ а сама трапеция в лю­бой момент проходила через ось винта и чтобы при этом за один обо­рот вокруг d_i она поднялась на высоту шага S. Чтобы построить точки, принадлежащие винтовой нитке, например, для момента, когда трапеция переместится из начального положения в положение, соответствующее четвёртому делению, отмечаем на горизонтальной проекции её точки a₄b₄e₄c₄. Для определения вертикальных проекций этих точек проекти­руем их на соответствующие линии деления шага,—получим a'₄b'₄e'₄c'₄.

Продолжая таким образом построение и для других положений про­филя резьбы, определим остальные точки винтовой нитки. Если винт разрезать секущей плоскостью NE так, как показано на чертеже, то на­чальной точкой, принадлежащей контуру сечения, как видно, будет точка b'₁

Чтобы получить, например, точку К, производим построение трапе­ции на вертикальной проекции соответственно горизонтальной её проек­ции на линии деления 2—10. Секущая плоскость NE пересечёт сторону BE трапеции в точке k'₂ Далее,проектируя к'₂ на линию деления 2—10, полу­чим точку k₂.  Так строятся и остальные точки контура сечения.

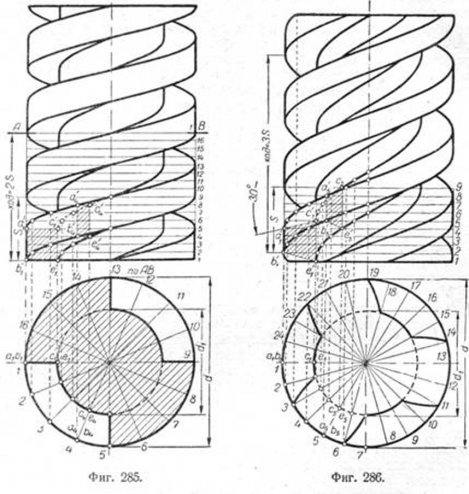
Построение винтовой поверхности для двухзаходной прямоуголь­ной резьбы (фиг. 285). Как видно из чертежа, операции построе­ния такие же, как и для однозаходных винтов. В отличие от предыду­щих примеров, делим на равное число частей не шаг, а ход так, как показано на фиг. 285. При этом перемещаемый вокруг оси винта профиль резьбы за один оборот поднимется не на шаг, как это было раньше, а на два шага.

Чтобы получить, например, точки, принадлежащие положению про­филя, когда последний совпадает с линией деления 4—12, т. е. c₄a₄b₄e₄ проектируем эти точки на вертикальную проекцию, получим b'₄e'₄. как a'₁b'₁ = c'₁e'₁ перпендикулярны к плоскости H, то,очевидно, a'₁b'₁= = c'₁e'₁ = a'₄b'₄ = c'₄e'₄. Отсюда легко могут быть построены точки a'₄ и c'₄. Дальнейший ход построения ясен. Поперечное сечение при данной секущей плоскости AB изобразится так, как показано на чертеже. Если

плоскость разреза перенести выше на 1/8 хода, то сечение повернётся по

часовой стрелке на угол 45°. Если секущую плоскость провести на 1/4

хода, то сечение повернётся в ту же сторону на 90°.

Построение винтовой поверхности трёхзаходного винта с резьбой трапецоидального профиля (фиг. 286.) Разделим большую окруж­ность на 24 части. На такое же число частей разделим и ход. В данном случае поделена лишь третья часть хода, равная шагу S. В принципе построение такой винтовой поверхноста ничем не отличается от построе­ния для двухзаходного винта, поэтому на пояснениях останавливаться не будем. Нетрудно заметить, что чем больше заходов на винте, тем круче подъём винтовой нитки и, следовательно, гайка, навинчиваемая на трёхзаходный винт при равных шагах 5, за один полный оборот её поднимется или опустится на величину, в три раза большую, чем при однозаходном винте.

Трёхзаходные и двухзаходные винты находят применение в прессах, червячной передаче и других конструкциях.

Вентили, задвижки, краны, слесарные тиски и подобные им изделия

снабжаются однозаходными винтами с прямоугольной, а иногда с трапецоидальной резьбой.

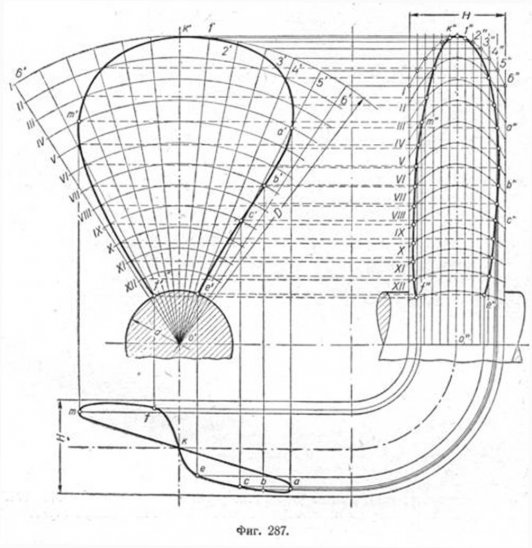
Вычерчивание лопасти судового винта. Пусть даны главный вид лопасти винта, диаметр винта D, шаг H и диаметр вала d. Требуется построить проекции лопасти винта (фиг. 287).

Проводим из центра О' ряд произвольных концентрических дуг I, II, III... XII. Затем из того же центра О' откладываем вправо и влево равные углы k'o'6' так, чтобы очертание лопасти винта не выходило за пределы лучей o'6'. Делим дугу 6'k'6' на произвольные, но равные части, в нашем примере на 12. Через точки деления 1', 2'...6' проводим из центра о' лучи o'1'; o'2'...o'6'. Строим профильную проекцию оси лопасти. Откладываем симметрично проведённой оси размер шага винта, равный H. Делим шаг винта И на такое же число частей, на какое была разделена дуга 6'k'6', т. е. на 12. Через точки деления проводим вертикальные прямые и переносим на них с главного вида дуги окружностей I, II, III...XII. Их проекции на виде слева будут частями синусоид. Нахождение точек синусоиды отмечено на кривой I точками 7", 2", 3"... 6". Построение остальных кривых II, III... XII показано без обозначения точек.

Для построения самого очертания лопасти на этом виде нужно пе­ренести с главного вида на синусоиды соответствующие точки пересече­ния дуг с контуром. Так, например, точке а' будет соответствовать а", точке b'-b" и т. д. Найденные точки соединяем между собой. Вид сверху может быть построен без затруднений, что видно из чертежа.