Техническое черчение

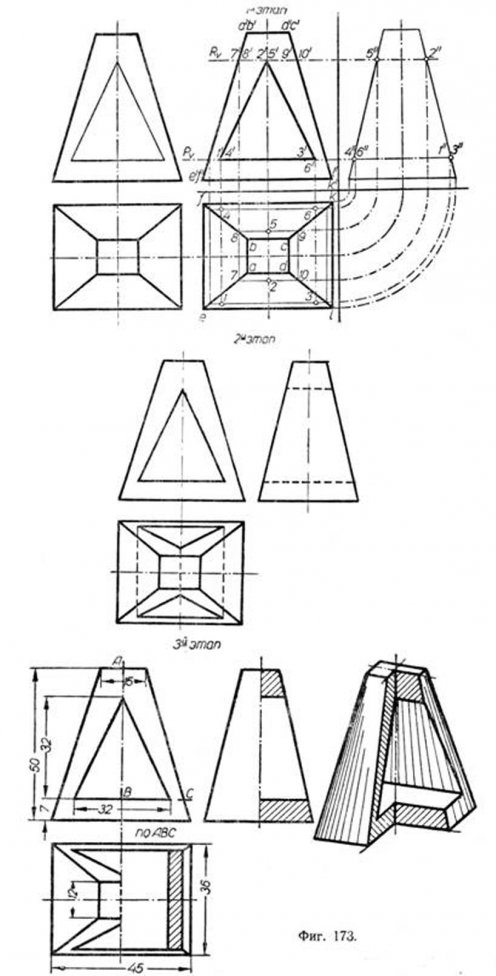
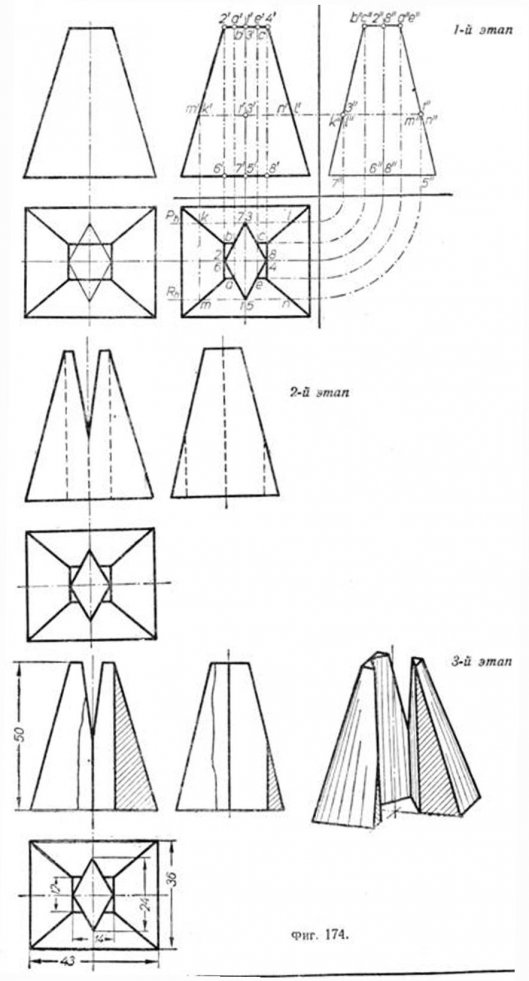
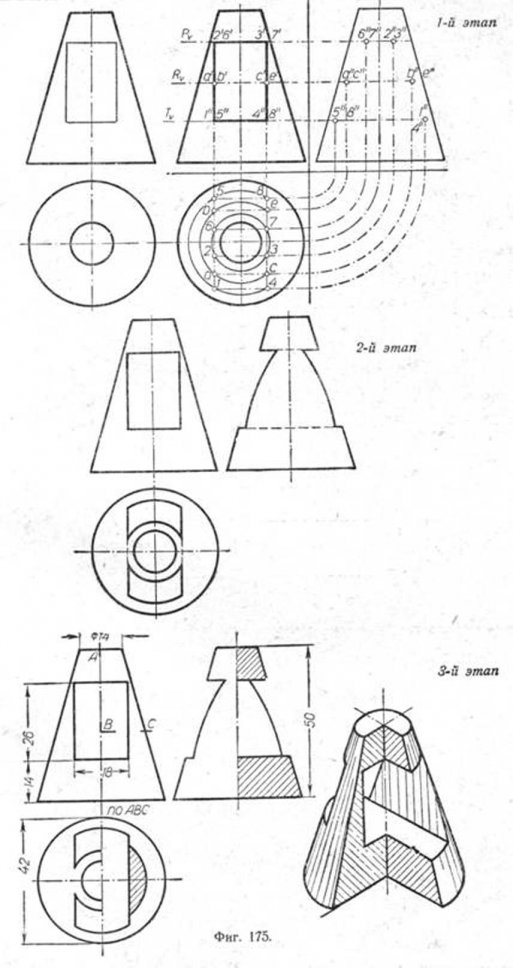
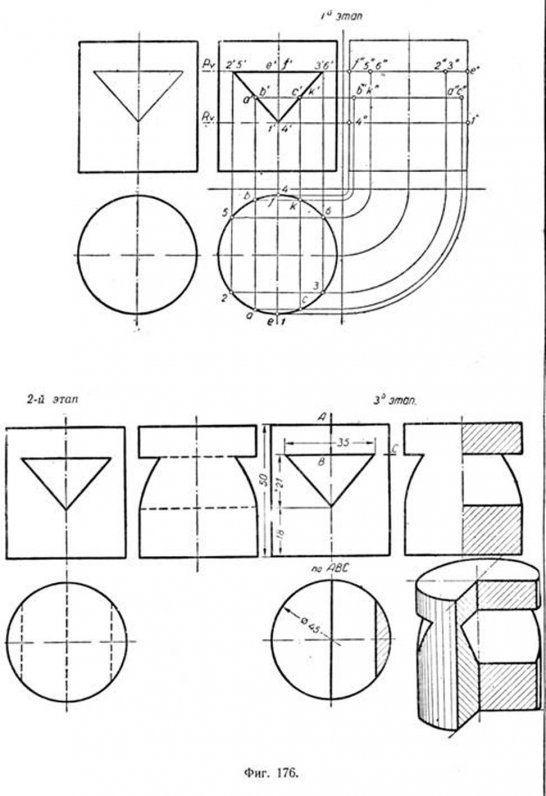
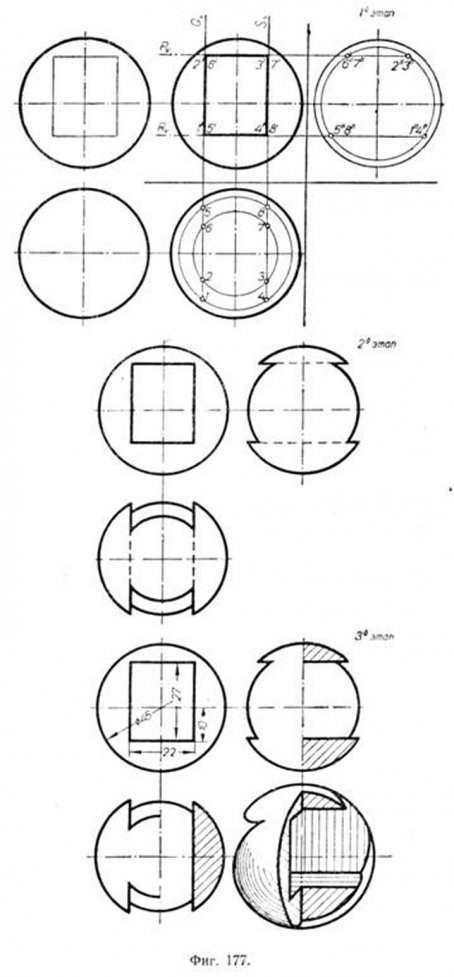
Построение трёх проекций с разрезами пирамиды с прямоугольным основанием и пересекающей её призмы с треугольным основанием (фиг. 173). В данном положений призма пересечёт переднюю и заднюю грани пирамиды по треугольникам, имеющим общую вертикальную проекцию.

Рассекая призму и пирамиду горизонтальной плоскостью R (1-й этап), получим фигуру сечения пирамиды—прямоугольник 7—8—9—10, изображённый на плане в натуральную величйну. Так как плоскость R, отмеченная следом R_v, проведена через ребро 2'-5' то это ребро пересечёт контур сечения 7—8—9—10 в точках 2 и 5. Точно так же будут построены точки пересечения 1—4, а затем 3—6. Фигурами, по которым призма пересекла данную пирамиду, являются треугольники 1—2—3 на грани EADL и 4—6—5 на грани FBCK. Второй этап показывает изображение пересекающихся пирамиды и призмы без разрезов. Для выявления внутренних очертаний уместно сделать разрезы. Для горизонтальной и профильной проекций они показаны на чертеже (3-й этап). Для большей наглядности рядом с ортогональными проекциями приведена пирамида в аксонометрической проекции.

Возьмём ту же пирамиду и пересечём её призмой, имеющей в основании ромб (фиг. 174).

Для решения этой задачи воспользуемся фронтальными секущими плоскостями. Чтобы определить вертикальные проекции точек встречи рёбер призмы с поверхностью пирамиды, удобно провести через рёбра 1—5 и 3—7 фронтальные плоскости P и R. Эти плоскости пересекут грани пирамиды по прямым MN и KL. Точка 7 расположится на прямой MN, а точка З—на прямой KL. При наличии третьей проекции решение задачи упрощается.

Для выявления внутренних очертаний применены вырывы (3-й этап), там же показана аксонометрия фигуры.

Пересечение усечённого конуса призмой, имеющей в основании прямоугольник (фиг. 175). Горизонтальные грани призмы 2—6—7—3 и 1—5—8—4 пересекут конус по дугам окружностей, а профильные грани 1—2—6—5 и 3—4—8—7 по гиперболам. В первом этапе при вычерчивании дано построение горизонтальных и профильных проекций точек 1, 2, 3, 4, 5, 6, 7 и 8, принадлежащих окружностям и гипер­болам сечения, а также точек А, В, С и Е, определяющих гиперболы.

Во втором этапе при вычерчивании соединены проекции найденных точек. Видимые линии обведены контурными, невидимые—штриховыми линиями. Все вспомогательные линии удалены, оставлены лишь главные оси.

В третьем этапе горизонтальная и профильная проекции показаны с разрезами для выявления очертаний линий пересечения тел внутри конуса. Для большей наглядности рядом с ортогональными проекциями показан тот же конус в аксонометрии с вертикально-поперечным разрезом.

Пересечение прямого цилиндра с призмой (фиг. 176). Горизонтальные проекции точек пересечения определяются, как обычно, проведением горизонтальных секущих плоскостей: P—через рёбра призмы 2—5 и 3—6 и Q—через ребро 1—4. Но можно обойтись и без них, так как горизонтальные проекции точек пересечения совпадают с окружностями оснований цилиндра. Построение профильных проекций точек указывалось ранее.

Пересечение шара прямоугольной призмой (фиг. 177). Известно, что всякая плоскость пересекает поверхность шара по окружности. Воспользуемся этим свойством шара. Грани призмы, пересекающей шар, как видно из задания, расположены параллельно горизонтальной плоскости проекций (грани 2—3—7—6 и 1—4—8—5) и параллельны профильной плоскости проекций (грани 1—2—6—5 и 4—3—8—7).

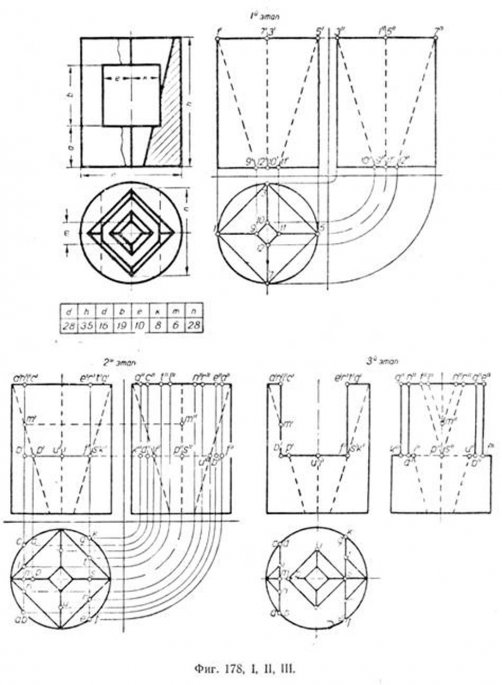
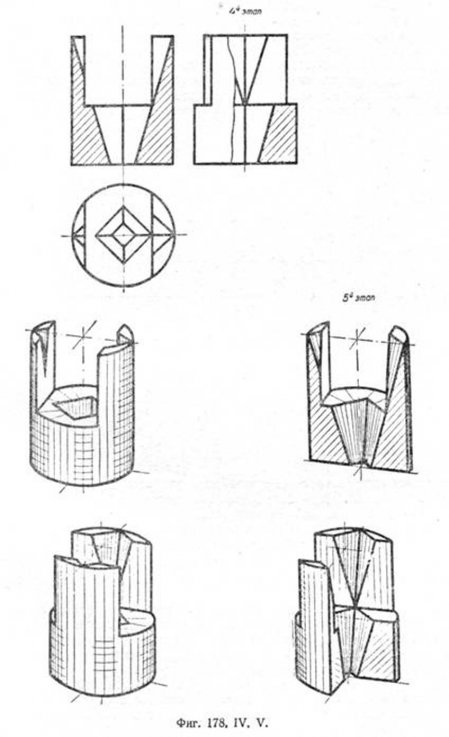
Такое расположение граней упрощает решение задачи в том отношении, что плоскости, проходящие через грани, пересекут поверхность шара по окружностям, проектирующимся на соответственных плоскостях проекций в натуральную величину. Радиусами этих окружностей будут полухорды, сливающиеся с вертикальными следами секущих плоскостей.

В первом этапе при вычерчивании показано построение проекций основных точек, принадлежащих окружностям сечений и соответственным прямым. В третьем этапе даны разрезы: вертикально-поперечный и горизонтальный. Для наглядности рядом дано аксонометрическое изображение шара с вертикально-поперечным разрезом.

На фиг. 178 дано более сложное пересечение прямого кругового цилиндра с пирамидой и призмой. Пирамида имеет квадратное основание и одноосна с цилиндром, а ось прямоугольной призмы перпендикулярна

к оси цилиндра. Требуется построить фигуру по заданным размерам (указанным в табличке).

Построение разбито на пять этапов и ясно из чертежа.