Техническое черчение

Прежде чем приступить к построению проекций геометрических тел, ознакомимся со способами нахождения проекций точек, расположен­ных на поверхностях мно­гогранников и тел враще­ния.

Нахождение проекций отдельных точек, располо­женных на поверхности тел, рассмотрим на трёх про­стейших геометрических формах: пирамиде, конусе и шаре. Нахождение гори­зонтальных проекций точек при заданных вертикальных их проекциях рассмотрим одновременно для пирамиды и конуса.

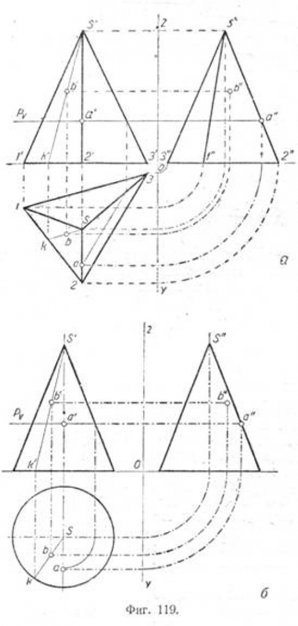
Пусть пирамида и ко­нус (фиг. 119, а, б) даны двумя своими проекциями, а точки А и В, лежащие на поверхностях этих тел, за­даны своими вертикальными проекциями а' и b'. Требу­ется найти горизонтальные и профильные проекции этих точек.

Такие задачи можно ре­шать следующим способом: на поверхности тел через заданную точку и вершину фигуры проводится прямая линия и затем строятся про­екции этой прямой. Искомая горизонтальная проекция точки будет лежать на го­ризонтальной проекции пря­мой. На фиг. 119, а и 119, б через точку b' проведена вертикальная проекция s'k' вспомогательной прямой ли­нии SK. Как видно, верти­кальной проекции s'k' со­ответствует горизонтальная проекция sk, что позволяет построить горизонтальную проекцию точки В. После этого легко построить профильную проекцию точки b''.

Чтобы построить горизонтальную проекцию точки А для пирамиды, нет необходимости строить вспомогательную прямую, так как точка А по заданию лежит на ребре S2. При наличии профильной проекции пирамиды легко построить профильную проекцию а" точки А на про­фильной проекции ребра S2 и по ней построить горизонтальную проек­цию а. Если профильной проекции на чертеже нет, надо использовать следующее основное положение начертательной геометрии: если точка а'

делит отрезок s'2' в отношении  s'a'/a'2'=m/n, то и на горизонтальнои проекции будет sa/a2=m/n. Вычислив по вертикальной проекции отношение ™, можно легко найти горизонтальную проекцию точки А на S2.

Эта задача может быть решена способом секущих плоскостей, являю­щимся общим для любой пространственной формы. Если провести через вертикальную проекцию точки А секущую горизонтальную плоскость P, то она пересечёт пирамиду по треугольнику, подобному треуголь­нику основания (фиг. 119, а), a ко­нус или шар (фиг. 119, б и 120) — по кругу. В этом случае треуголь­ник и круг сечения проектируются на горизонтальную плоскость в на­туральную величину. Горизонтальные проекции точки A расположены одновременно на перпендикулярах к оси ОХ, опущенных из соответ­ственных вертикальных проекций точки A.

При выполнении упражнений по проекционному черчению при­ходится довольно часто решать за­дачи на построение линий пересе­чения друг с другом двух поверх­ностей. Для выполнения этих по­строений необходимо уметь нахо­дить точки входа и выхода прямых, пересекающих заданные поверх­ности. Рассмотрим это построение на примерах.

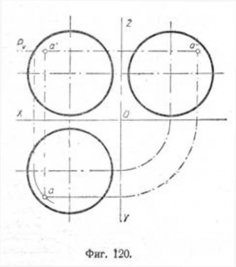
Пусть даны проекции пирамиды, конуса, шара и прямые EF и MN, пересекающие эти тела. Прямая EF перпендикулярна к плоскости V, а прямая MN—к плоскости W (фиг. 121, а, б, в). Требуется построить точки входа и выхода прямых, пересекающихся с заданными поверх­ностями.

Проводим через прямые EF и MN горизонтальные секущие плос­кости: через прямую EF—плоскость P, а через прямую MN—плоскость Q. Эти плоскости образуют на горизонтальной плоскости проекций пира­миды и конуса в сечении фигуры, подобные их основанию, а для шара— круг. Точки пересечения прямых с контурами сечения и будут искомымй точками входа и выхода: для прямой EF—точки А и С, а для прямой MN—точки К и L.

Если прямая пересекает поверхность шара, пирамиды или конуса перпендикулярно к плоскостй Н, то в этом случае проводят через за­данную прямую фронтальную плоскость. С целью упрощения построений для пирамиды и конуса полъзуются горизонтально-проектирующей плоскостью, которая должна непременно проходить через вершину фигуры.

Построив затем на вертикальной плоскости проекций, соответственно секущей плоскости, контуры сечения, находят точки входа и выхода.

Примеры решения задач на построение проекций фигур

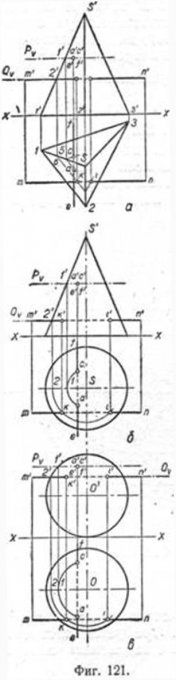
Пример 1. На фиг. 122 даны три про­екции пятиугольной усечённой пирамиды с открытым вырезом, образованным несколь­кими секущими плоскостями. Сечением этих плоскостей образовано на поверхности пира­миды ряд характерных точек: С, D, 1, 2, 3, 4, 5, 6, 7, 8, В и А, которые на вертикаль­ной плоскости проекций отмечены соответ­ственно: c', d', 1', 2', 3', 4', 5', 6', 7', 8', b' и a'. Требуется построить горизонтальные и профильные проекции этих точек.

Проекции точек А, В, С и D могут быть легко определены, так как они рас­положены на рёбрах пирамиды. Определим, для примера, горизонтальную проекцию точ­ки С, лежащую на ребре MN. Для этого проведём из точки с' проектирующую линию до пересечения с горизонтальной проекцией ребра MN и определим таким образом гори­зонтальную проекцию с точки С. Имея вер­тикальную и горизонтальную проекции этой точки, можно построить и профильную про­екцию с". По аналогии с этим, строим про­екции точек А, В и D. Проекции остальных точек 7, 2, 3, 4, 5, 6, 7 и 8 строим спосо­бом секущих плоскостей.

Чтобы построить горизонтальную про­екцию, например точки 7, проводим через неё секущую плоскость P, которая пересечёт пирамиду по пятиугольнику, подобному её основанию. Чтобы не затемнять чертежа по­строением пятиугольника, ограничимся одной из его сторон, проектирующейся на грань KETP. Пересечение контура сечения с го­ризонтальной проекцией ребра KP даст гори­зонтальную проекцию точки 1. Горизонталь­ные проекции точек 2, 3 определяются по аналогии, т. е. проведением через 2' и 3' плоскости R. Подобным образом произво­дится построение остальных точек. Имея го­ризонтальные и вертикальные проекции всех точек, нетрудно построить их профильные проекции. Законченное построение пирамиды приведено на фиг. 123. К изображениям в ортогональных проекциях добавлена аксонометрическая проекция этой пирамиды.

Пример 2. Построение в усечённом конусе вырезов,образованных четырьмя плоскостями, пересекающими поверхность конуса по основным кривым: окружности, эллипсу, параболе и гиперболе, приведено на фиг. 124. Горизонтальные проекции точек А и 1, лежащих на верти­кальной проекции линии контура конуса, легко определить без допол­нительных построений. Проекции остальных точек найдены проведением горизонтальных секущих плоскостей, обозначенных следами Pv,Rv и т. д.

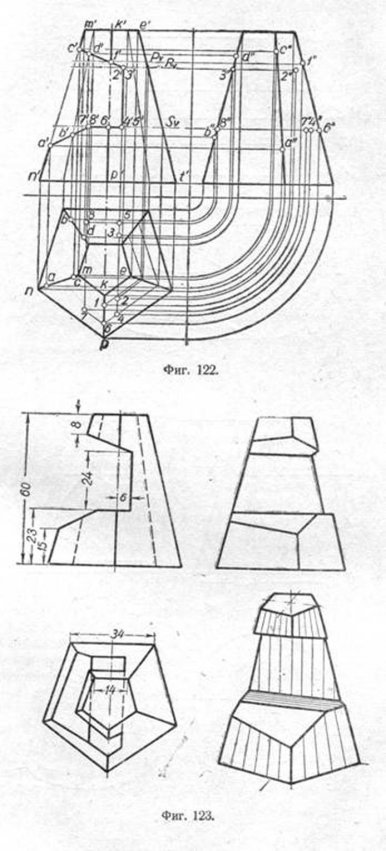
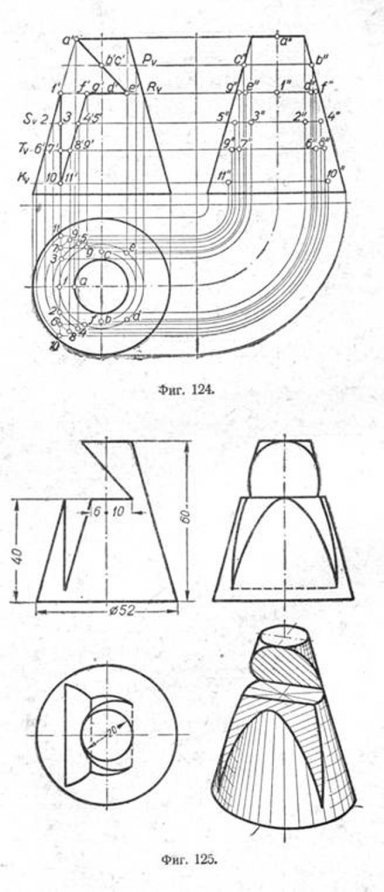
Определив горизонтальные проекции точек, нетрудно построить их профильные проекции. Последовательное соединение проекций точек кривых сечения показано на фиг. 125. Там же даны размеры конуса. Рядом с ортогональными проекциями показан тот же конус в диметрической проекции.