Техническое черчение

Непосредственное проектирование окружности на плоскость можно заменить проектированием описанного вокруг неё квадрата с последующим вписанием в проекцию квадрата проекции окружности. При этом используются следующие свойства параллельного проектирования этих фигур: 1) точка пересечения диагоналей проекции квадрата есть центр проекции окружности; 2) точками касания проекции окружности к проекции квадрата остаются средние точки сторон проекции квадрата; 3) на­правление сторон проекции квадрата является направлением двух сопряжённых диаметров проекции окружности.

Построим изометрическую проекцию окружности, лежащей в какой- нибудь координатной плоскости. Для этого возьмём куб, в грани которого впишем окружности. Куб расположим так, чтобы его грани были параллельны координатным плоскостям (фиг. 189).

Проекция куба имеет форму правильного шестиугольника, а проекцией каждой его грани является ромб.

Равенство ромбов—проекций квадратов—предопределяет и равенство эллипсов—проекций, вписанных в грани куба окружностей. Направления главных осей эллипса в изометрических проекциях совпадают с диагоналями ромба, в который вписан эллипс.

Следует запомнить простое правило нахождения большой и малой осей: малая ось всегда параллельна той оси, которой нет в названии плоскости эллипса. Так, например, если для эллипса плоскости OXZ нет названия оси OY, то малая ось этого эллипса параллельна оси OY. Большая ось всегда перпендикулярна к малой.

Можно это же условие выразить иначе: малая ось эллипса совпадает по направлению либо параллельна перпендикуляру к плоскости, в которой лежит спроектированная в эллипс окружность.

Чтобы построить эллипс по главным его осям, кроме направления, необходимы и размеры этих осей.

Как известно, независимо от положения плоскости проекций, большая ось эллипса всегда равна величине диаметра окружности, а малая в изометрической проекции равна 0,58 диаметра окружности. Прибли­жённо можно принять отношение между осями эллипса, равным 3:5.

Если построение окружности выполняется в масштабе 1,22:1, то при построении большой оси надо взять 1,22 d, а для малой ³/₅ этой вели­чины, т. е. 0,725 d.

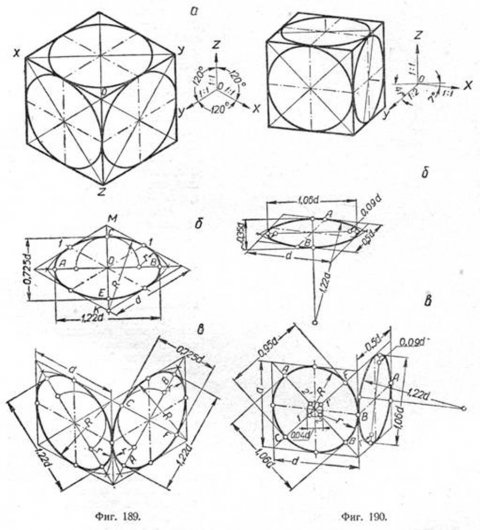
В практике часто вместо построения эллипсов лекальные кривые за­меняют циркульными и строят овал с тем же отношением 3:5 между главными осями.

На фиг. 189,б и в приведён способ построения овалов, заменяющих вписанные эллипсы. На одном чертеже овал вписан в ромб, соответ­ствующий горизонтальной грани куба, а на втором—двум боковым граням.

На фиг. 190 дана диметрическая прямоугольная проекция окруж­ности. Свойства, перечисленные в предыдущем случае, остаются в силе и здесь.

Эллипс, в который проектируется окружность, лежащая на передней грани куба, имеет, как и в случае изометрических проекций, главные оси, сливающиеся с диагоналями куба. Конечные точки осей могут быть определены как точки, делящие каждую из полудиагоналей ромба на части в отношении 7:10.

Для боковой грани и для грани верхнего основания куба направление малой оси эллипса параллельно аксонометриче­ской оси OY. Зная направление малых осей эллипсов, легко определить направление больших осей.

Для боковой грани боль­шая ось наклонена к оси OZ на угол 7°, а для грани верх­него основания большая ось будет горизонтальной прямой.

При проектировании в масштабе 1,06:1 длина боль­шой оси эллипса равна 1,06 d, где d  — диаметр окружности.

Что касается малой оси, то для фронтальной грани она равна 0,89, т. е. около 0,9 большой оси. Для граней бо­ковой и горизонтальной малая ось принимается равной 0,35 ребра куба или 1/3 большой оси эллипса.

Практически в этом слу­чае вместо эллипсов можно строить овалы.

На фиг. 190, б и в пока­заны способы построения ова­лов для каждой грани от­дельно.

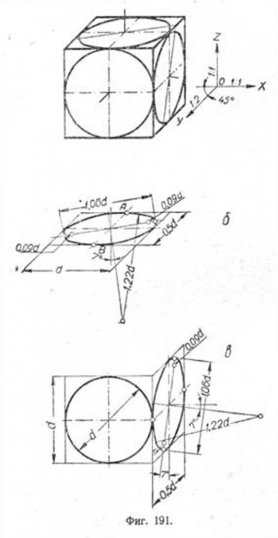
И, наконец, при косо­угольном проектировании диметрическая проекция фрон­тальной грани куба проекти­руется без искажений; очевидно, и окружность, вписанная в эту грань, проектируется в окружность (фиг. 191, а и в).

Боковая грань и грань верхнего основания куба по­чти не отличаются по форме от соответствующих граней, построенных в прямоугольной проекции.

Овалы в этом случае вычерчиваются почти так же, как и на соот­ветственных гранях куба предыдущего случая.