| Построение истинной величины наклонного сечения |
 |
|
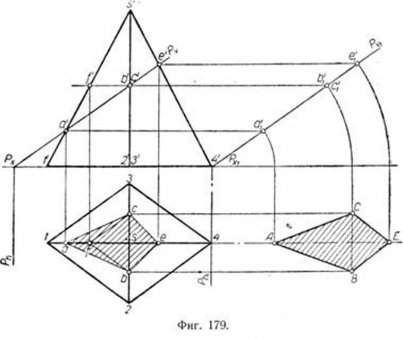
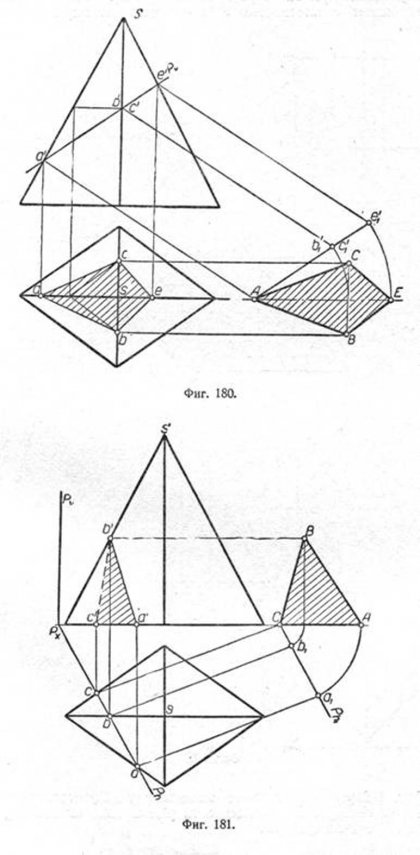
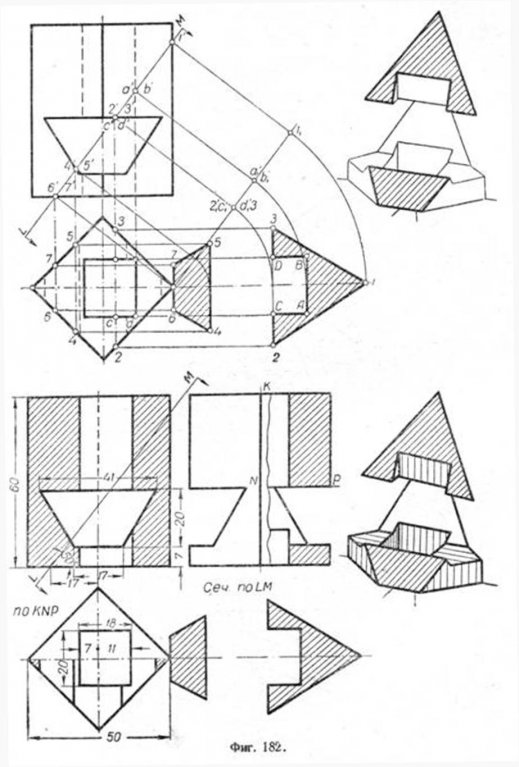
В курсах начертательной геометрии рассматривается ряд способов нахождения истинной величины сечения фигуры, в частности, способ совмещения. Рассмотрим несколько примеров. Пример 1. Пусть четырёхгранная пирамида пересекается вертикально-проектирующей плоскостью Р. Требуется определить истинную величину сечения (фиг. 179). Плоскость P пересекает пирамиду по четырёхугольнику a'b'e'c' - аbес. Чтобы определить истинную величину сечения этой фигуры, необходимо совместить её с одной из плоскостей проекций. Выбор плоскости совмещения диктуется удобством построения сечения. В данном случае удобнее произвести построение на горизонтальной плоскости проекций. Чтобы не затемнять построениями горизонтальной проекции пирамиды, перенесём секущую плоскость P с точками контура сечения параллельно первоначальному её положению. Плоскость отмечена вертикальным следом PV1 , точкой схода следов РХ1 и горизонтальным следом Ph1 . Далее совмещаем плоскость P с горизонтальной плоскостью проекций и получаем истинную величину сечения фигуры. Она отмечена буквами ABEC. В целях сокращения места и операций при построении истинной величины сечения, можно перенос контура сечения сделать так, как зто показано на фиг. 180. Отмечаем на продолжении горизонтальной оси фигуры в желаемом месте одну из точек, принадлежащих контуру сечения фигуры и принимаем её за совмещённую точку. В этом примере удобнее взять точку a', а, совмещённое положение которой обозначено буквой А. Затем переносим остальные точки контура сечения. Они отмечены буквами b'1, c'1,e'1. При этом Ae'1 ll a'e'. Затем контур сечения совмещаем с горизонтальной плоскостью и таким образом находим истинную величину сечения фигуры ABEC. Пример 2. На фиг. 181 приведено построение истинной величины сечения для случая, когда пирамида пересечена горизонтально-проектирующей плоскостью. Здесь тоже сделан перенос контура сечения параллельно первоначальному его положению. Отмечаем на оси проекций точку С. Проводим через точку С прямую Ca1 параллельную ca. Строим точки Ь1 и a1 Затем плоскость сечения совмещаем с плоскостью V и находим истинную величину сечения CBA. На фиг. 182 рассмотрен более сложный случай построения натуральной величины сечения. Для наглядности рядом дано аксонометрическое изображение сечения фигуры.
|