|
Линиями перехода в курсе черчения называются линии, по которым пересекаются между собою поверхности.
Теории построения линий перехода для различных поверхностей уделяется много внимания в курсах начертательной геометрии, здесь этот вопрос рассматривается кратко.
В случае пересечения осей двух тел вращения применяется способ шаровых поверхностей. Рассмотрим его на примере построения пересечения двух цилиндров, оси которых лежат в одной плоскости.
Пусть даны: барабан диаметром D, цилиндрический штуцер диаметром d и точка 0 пересечения осей обоих цилиндров (фиг. 170). Требуется построить линию перехода.
Точки 1 и 5 легко определяются: они лежат на пересечении крайних образующих малого цилиндра с верхней образующей большого. Каждая следующая промежуточная точка линии перехода будет определяться окружностью пересечения шара с любым из цилиндров. На приведённом чертеже эти окружности будут изображаться: для малого цилиндра— горизонтальными прямыми mn, ba и т. д., а для большого-вертикальными ks, c4, e2 и т. д. Пересечение этих окружностей и даёт искомые точки линии перехода. Например, шар радиуса Ос пересечёт малый цилиндр по окружности, проекцией которой является прямая ba, а большой—по дугам окружности 4c6 и 2e8. Пересечение этих дуг даёт точки 4 и 6, 2 и 8.
Для определения нижних точек линии перехода, т. е. точек 3 и 7, построим шар радиусом D/2- касательный к большому цилиндру. Проекция этого шара—окружность с радиусом D/2 — пересекает продолжение
крайних образующих малого цилиндра в двух точках n и m и касается большого—по окружности ks. Пересечение mn и ks даёт искомые точки: З—на передней стороне боковой поверхности цилиндра, 7—на противоположной стороне. Полученные точки соединяем кривой одинаковой толщины.
Справа на этом же чертеже изображён штуцер такого же диаметра, как и в предыдущем примере, с той лишь разницей, что он соединяется с барабаном не впритык, а по кривой pадиуса R. Построение точек
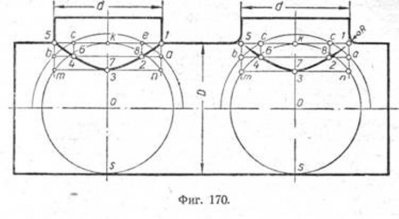
линии перехода выполняется так же, как и для штуцера, изображённого слева. Линия перехода, по мере подхода к точкам 1 и 5, меняет свою толщину и как бы сводится на нет. Целесообразность применения способа шаровых сечений очевидна. Задача здесь решается без дополнительных проекций.
Если геометрические оси тел вращения не пересекаются, то в этом случае надо пользоваться способом последовательного нахождения точек встречи образующих одной поверхности с другой. Рассмотрим случай
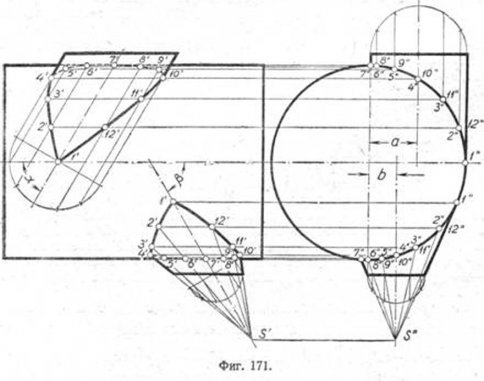
пересечения цилиндрического и конического штуцеров, оси которых составляют с осью барабана углы наклона а и ? и не пересекаются с осью основного цилиндра (фиг. 171). Для построения линии перехода цилиндрического штуцера, ось которого наклонена к барабану под углом а, делим окружность сечения, перпендикулярного к его оси, на некоторое число равных частей, например на 12. Проводим образующие через точки деления на вертикальной и профильной плоскостях проекций и нумеруем их. Образующие штуцера пересекаются на профильной проекции с корпусом барабана в точках 1", 2", 3"...12". Переносим эти точки на соответствующие образующие вертикальной проекции. Полученные точки 1', 2', 3' и т. д. соединяем между собой сначала от руки, а затем по лекалу. Эта кривая и будет линией перехода пересечения цилиндрического штуцера с барабаном.
Внизу, справа на чертеже, дано построение линии перехода пересечения конического штуцера с цилиндром. На поверхности конуса проводим образующие, отстоящие друг от друга на равных расстояниях. Точки их встречи с поверхностью цилиндра 1", 2", 3"...12" определяем на профильной проекции. Затем проекции найденных точек переносим на соответствующие образующие вертикальной проекции и соединяем их между собой сначала от руки, затем по лекалу.
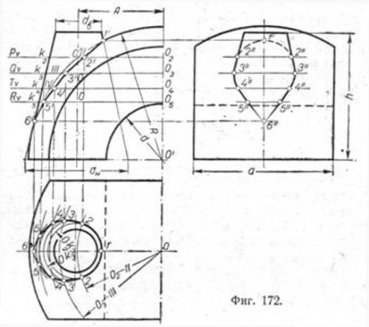 Построение линии перехода крышки подшипника, представляющей собой часть сферы, с коническим приливом (фиг. 172). Горизонтальные оси сферы и прилива лежат во фронтальной плоскости. В этом примере для нахождения линии перехода применён способ параллельных секущих плоскостей. Построение линии перехода крышки подшипника, представляющей собой часть сферы, с коническим приливом (фиг. 172). Горизонтальные оси сферы и прилива лежат во фронтальной плоскости. В этом примере для нахождения линии перехода применён способ параллельных секущих плоскостей.
Точки 1 и 6 определяются как точки пересечения линий контуров шара и конуса на вертикальной плоскости проекций. Для построения других точек искомой кривой проводится ряд горизонтальных плоскостей, в промежутке
между точками 1' и 6'. На чертеже их следы отмечены буквами Pv , Qv, Tv и Rv. Каждая из этих плоскостей пересечёт одновременно и шар и конус по окружностям, которые спроектируются на горизонтальной плоскости в натуральную величину. Точки пересечения окружностей, лежащих в одной секущей плоскости, и определят проекции искомых точек.
На всех проекциях при обводке линий перехода, подходя к точке 6, следует сводить линию на нет, как это показано на чертеже.
|

