|
Геометрические кривые имеют большое практическое применение в машиностроительной и строительной технике при конструировании деталей машин, исследовании процессов в машинах и т. п.
Они разделяются на циркульные и лекальные. К первым относятся завитки, овалы и т. п.; ко вторым —эллипсы, гиперболы, спирали, рулеты, синусоидальные кривые и т. п.
Рассмотрим построение этих кривых.
А. Циркульные кривые
Завитки. Завиток представляет собой кривую, приближающуюся по форме к спирали, вычерченной дугами окружностей. Завитки бывают двух-, трёх-, четырёх- и многоцентровые.
Построение двухцентрового завитка. Для построения двухцентрового завитка (фиг. 78) задаёмся расстоянием с между центрами 1—2.
Через центры 1 и 2 проводим прямую, и из точки 1 описываем полуокружность радиуса с до пересечения с продолжением той же прямой в точке p. Затем из центра 2, описываем полуокружность радиуса 2c до пересечения с прямой qs в точке t. Далее снова переходим в центр 7, откуда строим полуокружность радиуса Зс до пересечения с прямой в точке q и т. д.
Построение трёхцентрового завитка. Для построения завитка, имеющего три центра 1> 2 и 3 (фиг. 79), находящихся на равных расстояниях с один от другого, необходимо предварительно построить равносторонний треугольник 7, 2, 3 и продолжить его стороны так, как это показано на фигуре.
Из центра 7 проводим дугу З—к радиусом 1—3, равным с, до пересечения с продолжением стороны 2—1. Затем из центра 2 описываем дугу кр радиусом, равным 2c, до пересечения с продолжением стороны 3—2 в точке p, после чего из центра 3 проводим дугу pq радиусом, равным Зс, до пересечения с продолжением стороны 1—3 в точке q. После этого возвращаемся в центр 1 и продолжаем построение в такой же последовательности, каждый раз увеличивая радиус дуги на величину с.
Построение многоцентровых завитков выполняется аналогично построению, приведённому на фиг. 80 и 81.
Овалы (коробовые кривые). Овалом называется замкнутая кривая, состоящая из сопряжённых дуг окружностей разных радиусов. Овалы по форме напоминают эллипсы. Поэтому в практике в тех случаях, когда требуется построить эллипс, нередко вычерчивают овал, так как построение его значительно проще. Приводим несколько способов построения овалов.
Построение овала по заданной большой оси AB делением её на три равные части (фиг. 82). Делим заданную ось AB на три равные части и описываем из точек деления 7 и 2, как из центров, окружности радиусом А—1, получим точки 3 и 4.
Центрами сопряжения дуг овала будут точки 7, 2, 3 и 4. Для нахождения точек сопряжения проводим из центра 3 прямые через точки 7 и 2, а из центра 4—прямые 4—1 и 4—2. Найденные точки а, b, с и e будут точками сопряжения дуг овала.
Из центров 7 и 2 проводим дуги радиусом 1—а, а из центров З—4—радиусом З—а.
Построение овала по заданной большой оси AB при условии, что расстояние между центрами O-1 и 0-2=1/4 AB (фиг. 83). Через центр овала О проводим малую ось перпендикулярно AB и из того же центра радиусом 0—1=1/20A описываем окружность. Пересечение последней с малой осью определит центры 3 и 4. Дальнейшее построение аналогично предыдущему.
Построение овала по заданной малой оси СЕ (фиг. 84). Через середину О заданной малой оси СЕ проводим перпендикулярно к ней большую ось овала. Из центра О описываем окружность радиусом ОС. Пересечение её с большой осью определит центры 7 и 2 дуг сопряжения аb и се. Центрами дуг aCc и bЕе соответственно будут точки E и C.
Построение овала по двум заданным осям AB и CD (фиг. 85). Соединяем концы осей прямой CB и из центра О описываем дугу радиуса OB до пересечения с малой осью в точке B'. Затем из точки С,
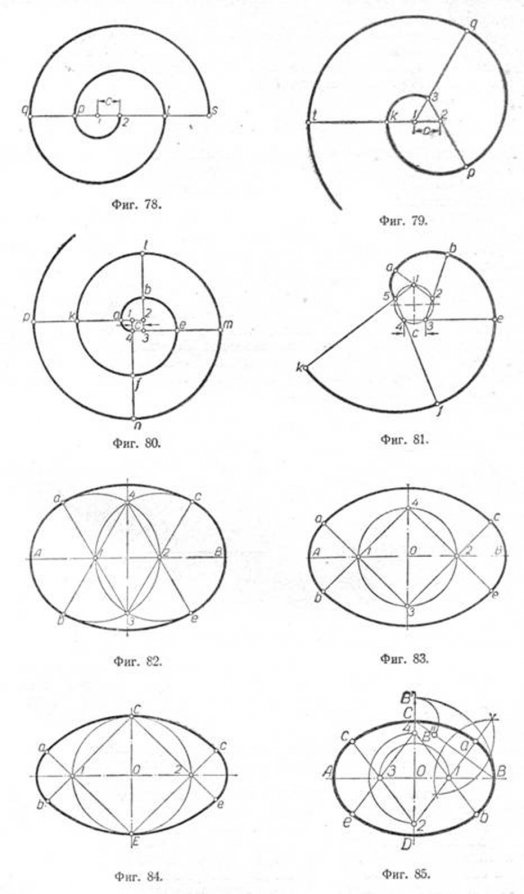
как из центра, проводим дугу радиуса CB' (разность полуосей) до пересечения с прямой CB в точке В".
Через середину отрезка B"B проводим перпендикуляр и продолжаем его до пересечения с полуосями OB и OD в точках 7 и 2, которые будут центрами сопряжения дуг аb и ас. Центры 3 и 4 определяются как точки, симметричные центрам 7 и 2.
Б. Лекальные кривые
Архимедова спираль (фиг. 86). Архимедова спираль представляет собою плоскую кривую, образованную точкой, равномерно движущейся по радиусу-вектору, который в то же время равномерно вращается вокруг неподвижной точки О.
Точки архимедовой спирали подчинены уравнению p=Rф, где p-pa- диус-вектор; ф—угол вращения; R—радиус окружности.
Пусть даны: центр О и радиус R окружности, ограничивающей кривую. Для построения по этим данным спирали разделим окружность и радиус на одно и то же число равных частей, например на 12.
Через точки деления радиуса проводим 12 концентрических окружностей, а через точки деления окружности 12 радиусов. Затем нумеруем окружности и радиусы, как показано на фиг. 86. Точки пересечения одноимённых концентрических окружностей и радиусов принадлежат кривой архимедовой спирали. Соединение точек О; 1', 2', 3' и т. д. производится при помощи лекала. По архимедовой спирали строится профиль фасонной фрезы.
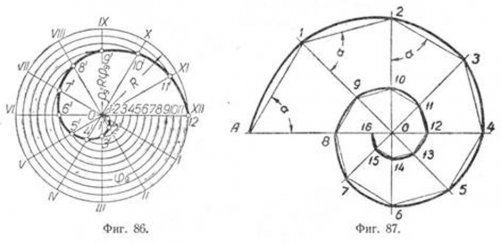
Логарифмическая спираль (фиг. 87). Логарифмическую спираль можно построить подобно спирали Архимеда как траекторию точки, перемещающейся по радиусу-вектору, в то время как сам радиус-вектор вращается вокруг неподвижной точки.
При этом, если угол поворота радиуса-вектора изменяется в арифметической прогрессии, то радиус-вектор изменяется в геометрической прогрессии.
Особенностью логарифмической спирали является то, что угол, образованный касательной k любой точке кривой с радиусом-вектором, есть величина постоянная. Этим свойством обладает также окружность, у которой этот угол составляет 45°. Следовательно, при одинаковых углах между радиус-векторами хорды, соединяющие концы их, образуют с соответственными радиусами равные углы.
Рассмотрим построение логарифмической спирали на примере. Пусть дан полюс О и отрезок прямой, равный OA, причём точка А принадлежит спирали. Требуется построить логарифмическую спираль (фиг. 87). Через полюс О проводим под равными углами друг к другу радиусы-векторы. В нашем примере они проведены под углом 45°. Из точки А под углом к радиусу-вектору OA строим хорду A1. Угол должен быть задан как параметр, характеризующий данную спираль; в этом примере а = 60°. Построенная хорда пересечёт смежный радиус-вектор в точке 1, также принадлежащей спирали. Проведя из точки 1 хорду под тем же углом, получим на радиусе-векторе 02 точку 2, принадлежащую этой спирали. Следующие точки находятся таким же образом. Получив точки первого оборота спирали, строим дальше в таком же порядке точки, принадлежащие второму, третьему и т. д. оборотам. Число оборотов для этой спирали бесконечно. Полюс О в этом случае является асимптотической точкой.
Логарифмическая спираль применяется в технике для затылования зубцов фасонных фрез, в частности зуборезных фрез.
Эллипс. Если прямой круговой конус рассечь наклонной плоскостью так, чтобы она пересекла все его образующие, то в плоскости сечения получится замкнутая кривая—эллипс; углы наклона секущей плоскости и образующей конуса к плоскости основания его будут иметь зависимость а < p (фиг. 88).
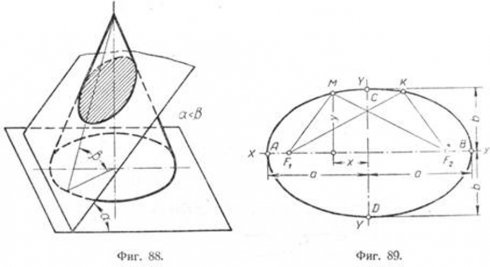
Эллипсом называется замкнутая плоская кривая, сумма расстояний каждой точки которой до двух точек (симметрично расположенных на большой оси относительно центра кривой), называемых фокусами, есть величина постоянная, равная большой оси эллипса (фиг. 89), т. е.
F1M + F2M = F1K+ F2K =AB.
Точки эллипса подчинены уравнению x2/a2+y2/b2=1, где а—малая полуось, b—большая полуось.
Существует несколько способов построения эллипса. Укажем на основные.
Построим эллипс по его главным осям—большой KL и малой — СE (фиг. 90).
Проводим из центра О произвольно ряд лучей, которые пересекут большую окружность в точках 1,3 и т. д., а малую—в точках 2,4 и т.д. Через точки пересечения на большой окружности проводим прямые, параллельные малой оси эллипса, а через точки пересечения на малой окружности—прямые, параллельные большой оси эллипса; полученные в пересечении точки а, b, С и т. д. принадлежат искомой кривой.
Рассмотрим эллипс как прямоугольную проекцию окружности. Два диаметра эллипса, являющиеся проекцией двух взаимно перпендикулярных диаметров окружности, называются сопряжёнными диаметрами. Обратим внимание на одно свойство отрезков сторон параллелограмма, построенного на сопряжённых диаметрах эллипса. Рассмотрим окружность с описанным вокруг
неё квадратом (фиг. 91). Проведём через произвольную точку E хорду BE и секущую AM.
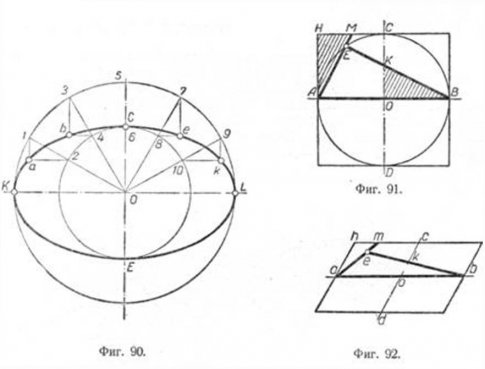
Треугольники OKB и AHМ равны. У них OB =AH, а кут НАМ равен куту KBO.
Следовательно, OK=HM. Так как OC=GH, OK/OC=HM/CH,
отрезок HМ составляет такую же часть отрезка НС, как отрезок OK отрезка ОС.
Как известно, прямоугольное проектирование не нарушит этих отношений (фиг. 92): квадрат спроектируется в общем случае в параллелограмм, окружность—в эллипс, точка E на окружности—в точку e на эллипсе, причём
OK/OC=hm/hc=HM/HC
На основании этого имеем способ построения точек эллипса по данной паре сопряжённых диаметров.
Сначала рассмотрим частный случай, когда сопряжённые диаметры KL и ЕМ пересекаются под прямым углом (фиг. 93). Построим прямоугольник по точкам К, Е, L и M и разделим большую сторону и малую ось на произвольное число равных частей, например на восемь. Через конечные точки большой оси К и L проводим ряд лучей, соединяющих эти точки с точками 1', 2', 3' и т. д. (деления стороны прямоугольника), и через точки 1, 2, 3 (деления малой полуоси). Лучи проводим до их взаимного пересечения. Полученные при этом точки a, b, с и т. д. принадлежат искомой кривой.
Рассмотрим теперь общий случай, когда угол между сопряжёнными диаметрами не прямой и эллипс надо вписать в параллелограмм. Задачу эту решим для случая построения диметрической проекции окружности (фиг. 94).
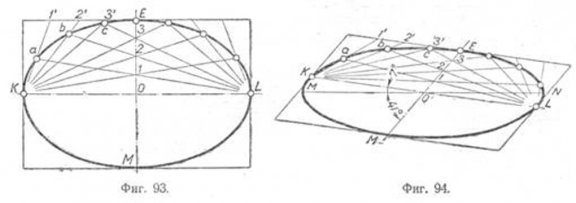
Проводим горизонтальную прямую. Берём на ней точку О. Строим в точке О сопряжённые диаметры эллипса KL и ЕМ: больший—под углом 7° к горизонтальной прямой, малый—под углом 41°. По большой оси откладываем LK = d, а по малой EM = 0,5LK = 0,5 d. Проведя через концевые точки К и L, E и M прямые, параллельные осям, получим параллелограмм.
Делим большую сторону параллелограмма и малую ось на равное число частей, например на восемь. Из точек К и L через точки деления проводим лучи; пересечение лучей К—1' и L- 1 дадут точку пересечения а; пересечение лучей K—2' и L—2—точку b и т. д.
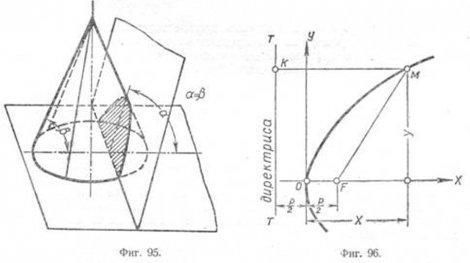
Парабола. Если прямой круговой конус рассечь плоскостью, параллельной какой-нибудь образующей (a = ?), то в сечении будет кривая- парабола (фиг. 95).
|
Параболой называется плоская кривая, все точки которой находятся на одинаковом расстоянии от данной точки, называемой фокусом, и от постоянной прямой—директрисы (фиг. 96), т. е. MK = MF.
Точки параболы подчинены управлению у2 = 2px, где р—расстояние от фокуса F до директрисы; 2p—параметр параболы.
|
Парабола находит применение в машиностроении (очертаниях кронштейнов, фермах, зубчатых колёсах, коренных подшипниках, сопряжениях рёбер стоек и подвесках подшипников), в оптике (линзы, прожекторные зеркала и т. п.).
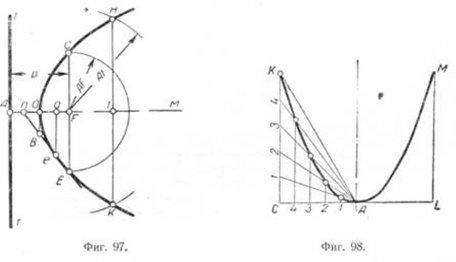
На фиг. 97 приведён способ построения параболы, основанный на определённых свойствах кривой.
Проводим взаимно перпендикулярные прямые TT и AM и принимаем одну из них—ТТ за директрису, а другую AМ—за ось параболы.На прямой AM откладываем отрезок AF равный P—выбранному нами расстоянию от фокуса до директрисы. Делим отрезок AF пополам. Середина его— точка О будет вершиной параболы, а точка ,F—фокусом.
Затем проводим через фокус F прямую, параллельную TT, и описываем из точки F дугу радиусом AF до пересечения с проведённой прямой; полученные точки С и E принадлежат параболе; AF=p; CE = CF + FE, но CF = EF=p, следовательно, CE = 2p.
Так же могут быть получены и другие точки параболы.
Возьмём, например, на оси произвольную точку 1 и проведём через неё вертикальную прямую. Сделав затем засечки на этой прямой дугой радиуса Л / из F, получим точки И и К, которые также принадлежат параболе.
Решим другую задачу. Пусть требуется через точку e провести касательную к параболе (фиг. 97). Для этого опускаем из точки e на ось параболы перпендикуляр ea. Откладываем On = Oa и соединяем точки n и e прямой, которая и будет искомой касательной.
В тех случаях, когда точка n выходит за пределы чертежа и провести прямую не представляется возможным, можно провести через вершину О касательную и на ней отложить отрезок OB, равный половине ae, и точку В соединить с точкой e. В этом случае прямая Be будет искомой касательной в точке e. Касательная к вершине параболы делит пополам любую касательную от точки её касания до точки пересечения с осью параболы.
Построим параболу по данным: вершине Л и одной из точек кривой—K (фиг. 98), Для построения промежуточных точек проводим из точек Л и К две взаимно перпендикулярные прямые до встречи в точке С и делим КС и АС на 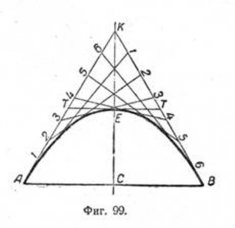 одинаковое число равных частей. Через точки деления на АС проводим прямые, параллельные CK, а из точки A—лучи к точкам деления на CK. Пересечение параллельных прямых с одноимёнными лучами определит точки, принадлежащие параболе. одинаковое число равных частей. Через точки деления на АС проводим прямые, параллельные CK, а из точки A—лучи к точкам деления на CK. Пересечение параллельных прямых с одноимёнными лучами определит точки, принадлежащие параболе.
На фиг. 99 приведено построение параболы по двум симметричным точкам А и В и точке К, заданной на оси параболы.
Строим по заданным точкам А, К и В треугольник AKB. Стороны AK и KB делим на одинаковое число равных частей, и точки деления соединяем следующим образом: нижнюю точку 1 прямой AK соединяем с верхней точкой 1 прямой KB, точку 2 прямой АК — с точкой 2 прямой KB и т. д. Проведённая таким образом сеть прямых образует систему касательных, определяющих форму кривой; огибающая этих касательных является параболой.
Пользуясь этим важным свойством касательной, в баллистике определяют наивысшую точку полёга пули или снаряда, теоретически принимая траекторию их полёта за параболу (фиг. 99).
Дальность полёта определяется хордой AB параболы, а угол вылета— углом наклона касательной AK к хорде AB.
Кубическая парабола (фиг. 100). Чтобы построить кубическую параболу, проходящую через точку Л, проводим прямую AB параллельно заданной оси ОХ, затем строим на ней, как на диаметре, полуокружность. Разделив прямые OB и AB на одинаковое число равных частей, в нашем примере на пять, получим на прямой OB точки 1, 2, 3 и 4, а на прямой AB—точки а, b, с, d, которые переносим на полуокружность
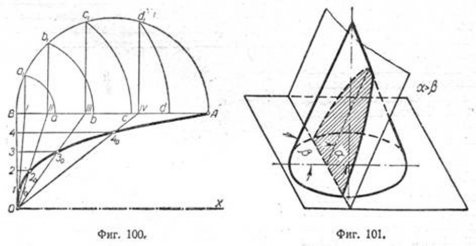
(точки а1, b1, с1, d1). Опускаем на прямую AB перпендикуляры a1I, b1II, c1III и т. д., а из точек 1, 2, 3, 4 проводим прямые, параллельные ОХ. Точки I, II, III и т. д. соединяем с точкой О лучами. Пересечения лучей с прямыми дадут соответственно точки /0, 20, 30, 40, принадлежащие кубической параболе. Найденные точки соединяем плавной кривой.
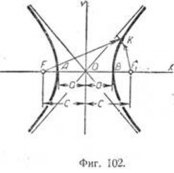
Гипербола. Если прямой круговой конус рассечь плоскостью, проходящей параллельно двум его образующим так, чтобы угол ? стал больше угла ?, то фигурой сечения будет плоская кривая—гипербола (фиг. 101). Гиперболой называется кривая, все точки которой обладают таким свойством: разность расстояний от каждой точки гиперболы до двух заданных точек, называемых фокусами, есть величина постоянная, равная расстоянию между вершинами гиперболы FK — F1K = AB=2a (фиг. 102).
Точки гиперболы подчинены уравнению
x2/a2 - y2/h2=1
где а — половина расстояния между вершинами гиперболы;
b=?c2 - a2;
с — половина расстояния между её фокусами.
Гипербола имеет две оси: действительную ось x и мнимую—y. При построении гиперболы пользуются асимптотами, внутри которых размещаются ветви гиперболы.
Асимптотами называются две прямые, проходящие через центр и касающиеся к гиперболе в бесконечности.
Если асимптоты образуют между собою угол 90°, то гиперболу называют равнобокой. Равнобокая гипербола имеет практическое применение при различных расчётах.
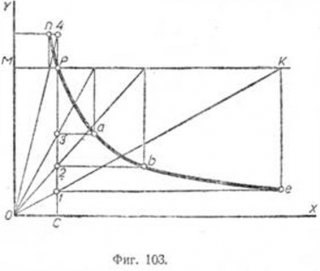
Построение равнобокой гиперболы (фиг. 103). Пусть даны асимптоты ОХ и ОУ и точка Я, принадлежащая ветви гиперболы. Проведём через точку P перпендикуляры MP и PC. На PC возьмём несколько произвольных точек 1, 2, 3 и 4У проведём через них прямые, параллельные OX; затем через эти же точки проведём лучи, выходящие из точки О, до пересечения с прямой МК, проведённой через точку P— параллельно асимптоте ОХ. Из полученных точек пересечения опускаем перпендикуляры на соответствующие прямые, проведённые параллельно асимптоте OX, через точки 1, 2, 3 и 4. Точки пересечения а, b и e будут принадлежать искомой кривой.
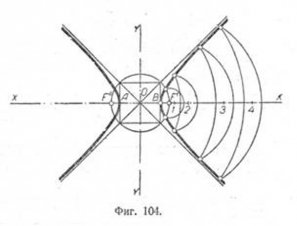 Построение гиперболы по вершинам А и В и фокусам F' и F" (фиг. 104). Для построения асимптот гиперболы описываем из О радиусом, равным OF', окружность, а через вершины А и В проводим прямые, параллельные мнимой оси ОУ. Точки пересечения проведённых прямых с окружностью определят направление асимптот. Для получения отдельных точек, через которые пройдёт кривая, возьмём несколько произвольных точек, расположенных на действительной оси гиперболы справа от фокуса F', и обозначим их цифрами 1, 2, 3 и 4. Расстояние между ними увеличиваем (произвольно) по мере их удаления от F'. Принимая расстояния 1 - A и 1—В за радиусы- векторы, описываем из F' и F'' взаимно пересекающиеся дуги, точки пересечения которых принадлежат кривой. Действительно, разнoсть радиусов-векторов является для всех рассматриваемых точек (1, 2, 3 и 4) величиной постоянной, равной расстоянию между вершинами гиперболы. Таким образом, радиусами-векторами для точки 4 будут отрезки А—4 и В—4, разность которых равна AB, что и соответствует основному свойству кривой. Построение точек для левой ветви гиперболы выполняется так же, как и для правой. Построение гиперболы по вершинам А и В и фокусам F' и F" (фиг. 104). Для построения асимптот гиперболы описываем из О радиусом, равным OF', окружность, а через вершины А и В проводим прямые, параллельные мнимой оси ОУ. Точки пересечения проведённых прямых с окружностью определят направление асимптот. Для получения отдельных точек, через которые пройдёт кривая, возьмём несколько произвольных точек, расположенных на действительной оси гиперболы справа от фокуса F', и обозначим их цифрами 1, 2, 3 и 4. Расстояние между ними увеличиваем (произвольно) по мере их удаления от F'. Принимая расстояния 1 - A и 1—В за радиусы- векторы, описываем из F' и F'' взаимно пересекающиеся дуги, точки пересечения которых принадлежат кривой. Действительно, разнoсть радиусов-векторов является для всех рассматриваемых точек (1, 2, 3 и 4) величиной постоянной, равной расстоянию между вершинами гиперболы. Таким образом, радиусами-векторами для точки 4 будут отрезки А—4 и В—4, разность которых равна AB, что и соответствует основному свойству кривой. Построение точек для левой ветви гиперболы выполняется так же, как и для правой.
Если прямые, проведённые через вершины А и В параллельно мнимой оси, пересекут окружность в равноудалённых от осей точках, то асимптоты будут взаимно перпендикулярны, а гипербола — равнобокой.
Циклоидальные кривые (рулеты). Циклоидальными кривыми называют траекторию точки круга, перекатывающегося без скольжения по прямой или неподвижному кругу. К этим кривым относят циклоиду, гипоциклоиду и эпициклоиду. Все они имеют практическое применение в машиностроении. Так, они используются при построении профилей зубцов цилиндрических, конических и винтовых зубчатых колёс.
Точка, описывающая при своём движении циклоидальную кривую, называется производящей. Окружность или прямая, по которым происходит перекатывание, называется направляющей.
Циклоида. Циклоидой называется кривая, которую описывает точка круга, катящегося без скольжения по прямой линии.
Пусть образующий круг диаметра d с взятой на нём производящей точкой К перекатывается по направляющей TT (фйг. 105). Точка К, перекатываясь вместе с кругом, опишет полный цикл кривой и снова придёт в соприкосновение с прямой ТТ. Расстояние между двумя последовательными положениями К на прямой TT соответствует полному
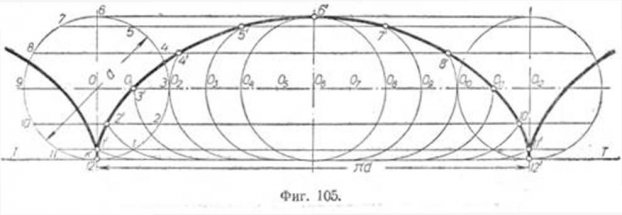
обороту кpyra и равно ?d. Чтобы определить промежуточные положения производящей точки в каждый момент, разделим прямую О0—012 на 12 равных частей. Точки Ol ,02, 03 и т. д. представляют последовательные положения центра образующего круга. Разделим и окружность на такое же число равных частей. Через точки деления проведём, параллельно направляющей, линии возвышения производящей точки.
Нетрудно представить, что при качении круга по направляющей расстояние между любой из этих точек и соответственным положением точки К остаётся неизменным.
Пусть центр окружности О переместится в О1. Образующий круг
пройдёт путь, равный длине дуги К—1= ?d/12. Точка К перейдёт в положение 1' на пересечении окружности, проведённой из О1 с первой линией возвышения производящей точки 1—11'.
Если центр окружности переместится в точку 02 , то производящая точка займёт положение точки 2' на пересечении окружности, проведённой из 02} со второй линией возвышения 2—10' и т. д.
Плавная кривая, соединяющая полученные точки, носит название нормальной циклоиды. Кроме нормальной, существуют циклоиды растянутые и сжатые.
Если взять точку К внутри круга, то такая точка опишет растянутую циклоиду. Пример построения растянутой циклоиды дан на фиг. 106.
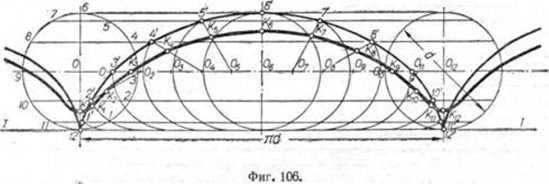
Здесь производящая точка К находится на том же радиусе, что и производящая точка нормальной циклоиды. Чтобы определить отдельные положения движущейся точки К, достаточно определить направление радиусов, на которых располагается точка К в моменты перемещения круга из центра О в О1 02 03 и т. д.
На каждом из этих радиусов необходимо отложить от точек 01 , 02, 03 и т. д. отрезки, равные ОК. Полученная при этом система точек определит форму кривой—растянутой циклоиды.
Пусть центр круга переместится в точку 04, тогда производящая точка нормальной циклоиды станет в точку 4'. Соединив точки 04 и 4' получим направление радиуса. Откладывая на радиусе 04—4' из точки 04 отрезок, равный OK, определим точку К4, принадлежащую растянутой циклоиде. Если точку К приближать к центру круга, то циклоиды таких производящих точек всё больше и больше будут растягиваться, приближаясь к линии 0 — 012, и, наконец, обратятся в прямую, когда точка К будет взята в центре круга О.
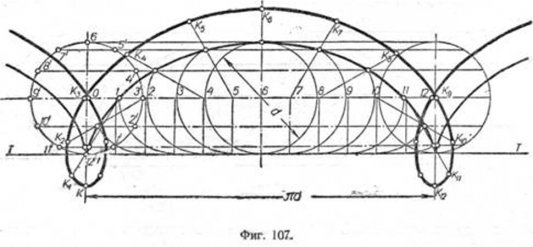
Если точку К удалять за пределы круга, то производящая точка будет описывать петли и форма циклоиды будет сжатой.
Подобный пример представлен на фиг. 107. Из чертежа видно, что способ построения сжатой циклоиды аналогичен построению растянутой циклоиды.
Эпициклоида. Эпициклоидой называется кривая, которую описывает точка круга, перекатывающегося без скольжения по направляющему кругу.
Пусть образующий круг диаметра d перекатывается по направляющему кругу диаметра D. Пусть точка а, лежащая на радиусе Oa, будет производящей (фиг. 108).
Построение точек эпициклоиды подобно построению циклоиды. При качении производящая точка опишет цикл кривой и после одного оборота круга переместится из точки а в точку 12, удалившись от первоначального положения по дуге направляющего круга на ?d.
В практике откладывают дугу путём построения в центре О угла а, равного 360° d/D.
Для определения промежуточных положений производящей точки делят образующий круг и дугу направляющего круга, соответственно углу ?, на 12 равных частей. Затем из центра О0 через точки деления образующего круга проводят концентрические дуги возвышения производящей точки, а через точки деления направляющего круга—лучи.
Пересечение лучей с линией центров определит двенадцать последовательных положений центра образующей круга. Как и в циклоиде, при перемещении образующего круга на 1/12 цикла, произойдёт перемещение его центра из О в О1 которому будет соответствовать первое положение производящей точки на дуге возвышения, отмеченное точкой 1. Если центр образующего круга переместится ещё на 1/12 своего пути и станет в точку 02, то образующий круг пройдёт путь а—2, равный длине дуги (2/12)?d направляющему кругу, а производящая точка займёт положение, отмеченное точкой 2'—на пересечении дуги, проведённой из центра 02 радиусом d/2, со второй дугой возвышения.
Производя такие же построения для последующих положений центра, определяют соответствующие положения производящей точки, а следовательно, и кривую—эпициклоиду.
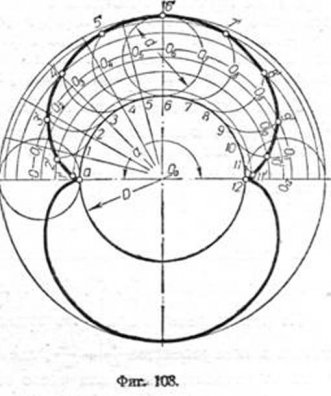
Если образующий круг будет перемещаться и дальше по направляющему, то производящая точка опишет ещё одну эпициклоиду.
В рассмотренном примере приведено построение эпициклоиды для соотношения диаметров образующего и направляющего кругов, равных
d/D=1/2. В этом случае производящая точка а после второго цикла
займёт своё исходное положение.
Это отношение показывает, что производящая точка а придёт в исходное положение на направляющем круге, когда производящий круг диаметра d сделает два оборота и обернётся вокруг направляющего круга один раз. Производящая точка а опишет при этом две эпициклоиды и совпадёт с направляющим кругом в двух диаметрально противоположных точках.
Предположим, что отношение d/D=2/3 .
В этом случае производящая точка а придёт в исходное положение после того, как производящий круг диаметра d, сделав три оборота, обернётся вокруг направляющего круга диаметра D два раза. Производящая точка а опишет три эпициклоиды и на пути перемещения совпадёт с направляющим кругом в трёх равноудалённых точках.
Когда отношение d/D есть целое число, например d/D=5/1, то производящая точка а займёт исходное положение на направляющем круге после того, как производящий круг диаметра, сделав один оборот, обернётся вокруг направляющего круга диаметра d пять раз. Производящая точка опишет при этом одну эпициклоиду и, перемещаясь, будет иметь с направляющим кругом только одну точку совмещения, соответствующую исходному её положению.
В практике встречаются отношения d/D, составляющие неправильную
дробь, как, например, 2/3, 5/3, 7/3 и т. д.
Из рассмотренных примеров видно, что отношение d/D можно представить в виде равенства d/D=n/n1 , где n1—число оборотов образующего
круга по направляющему или число эпициклоид, описанных производящей точкой, либо число касаний этой точки с направляющим кругом до совмещения её во всех этих случаях с начальным положением. Одновременно n показывает число перекатываний образующего круга по направляющему (до момента совмещения производящей точки с её начальным положением).
Гипоциклоида. Гипоциклоидой называется кривая, которую описывает производящая точка, лежащая на образующем круге, катящемся без скольжения, внутри другого круга, называемого направляющим.
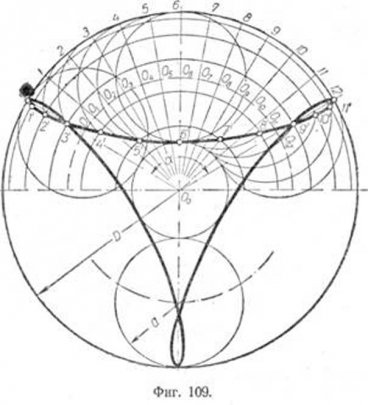
Построение точек гипоциклоиды производится тем же способом, что и эпициклоиды (фиг. 109).
Эвольвента (развёртка круга). Эвольвентой называется кривая, которая описывается любой точкой прямой, катящейся пo кругу без скольжения.
Образующей здесь является прямая, а направляющей—круг. Если гибкую нить, обёртывающую круг диаметром d (фиг. 110), разматывать с некоторым постоянным натяжением, то конец её, обозначенный точкой 1, опишет кривую 1, /, //, III ... VIII, называемую эвольвентой или развёрткой.
Отрезки нити 2—1, 3—II, 4—III и т. д.—касательные к точкам 2, 3, 4..., равны соответственным дугам 2—1, 3—1, 4—1 и т. д. развёртываемого круга.
Для построения эвольвенты разделим данную окружность на равное число частей, например восемь. Из точек деления проводим касательные перпендикулярно к радиусам. На прямой 1—VIII откладываем отрезок,
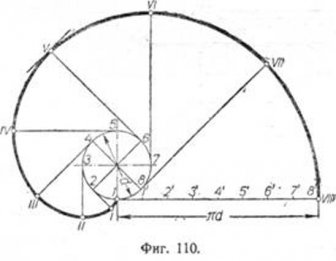
равный ?d, и делим его на 8 равных частей. На промежуточных касательных откладываем соответственные отрезки выпрямленных дуг. Так, например, на касательной к точке 2 откладываем отрезок, равный 1—1', и получим точку I. Отложив на касательной в точке 3 отрезок, равный 1-2', получим точку II и т. д.
Эвольвента применяется для вычерчивания профилей зубцов зубчатых колёс.
Кардиоида. Если через точку, взятую на окружности, провести во всех направлениях лучи, пересекающие эту окружность, и из каждой точки пересечения отложить вдоль каждого луча в обе стороны отрезки, равные диаметру этой окружности, то получим точки кривой, называемой кардиоидой. Для построения кардиоиды возьмём на окружности диаметра d точку К (фиг. 111) и проведём под произвольными углами a1, a2 т. д. лучи K1, K2, КЗ.
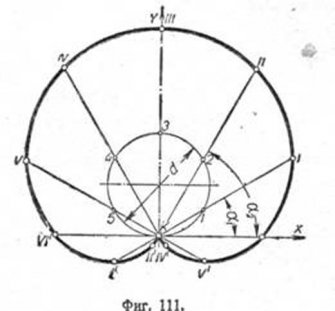
Из точек 1, 2, 3 и т. д. откладываем ня лучах в обе стороны отрезки, равные диаметру d. По одну сторону от точки К получим точки /, //, III и т. д., по другую—/', //', К, принадлежащие кардиоиде.
В машиностроении кардиоида применяется при изготовлении кулачков и других деталей.
Синусоида. Для построения синусоиды (фиг. 112) делим окружность на произвольное число равных частей, в данном примере на 12. На
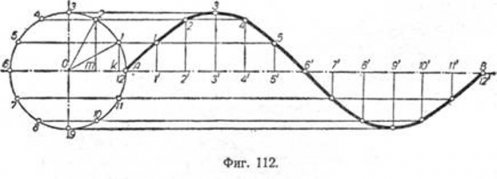
такое же число частей делим прямую АВ, величина которой равна длине окружности ?d. В точках деления прямой AB по перпендикулярам к ней откладываем полухорды 1к, 2m и т. д., пропорциональные синусам центральных углов к01, m02 и т. д. Полученные точки 1, 2, 3 и т. д. соединяем по лекалу плавной кривой. Синусоида может быть сжатой или растянутой. В первом случае AB<?d, во втором — AB>?d.
Синусоидальными кривыми пользуются при исследовании гармонических колебательных процессов, происходящих в электрических машинах, аппаратах, для построения кулачков и т. п.
Политропа. Политропой называется кривая, выраженная уравнением ухn=c, где c — постоянная величина. Для построения политропы по её показателю n и точке P, принадлежащей этой кривой (фиг. 113), проводим прямую OA под произвольным углом а к оси ОХ и прямую OB под углом ? к оси OY. Угол ? определяется из уравнения: 1+tg?= (l+ tg?)2. Затем через точку P проводим прямые параллельно осям ОХ и OY до пересечения с OA в точке а и с OY в точке е. Потом из точек а и e проводим к ОХ и ОУ под углом 45° прямые, засекающие точки а' и e'. Далее через полученные точки проводим прямые параллельно осям до их взаимного пересечения в точке 1, которая и будет принадлежать политропе.
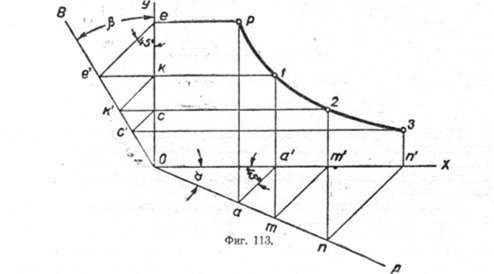
Чтобы построить точку 2, отмечаем на пересечении прямой e'l с осью OY точку К. Из точки К проводим параллельно прямой ee' прямую KK' из a'—прямую a'm параллельно Ра, а из m—прямую mm' параллельно aa'. Проведя затем из точек m' и к' прямые, параллельные осям OY и OX, получим на их пересечении точку 2. Остальные точки политропы строятся по аналогии.
Политропа применяется при исследовании тепловых двигателей (построение индикаторной диаграммы); при этом показатель степени n принимается в пределах 1,1 —1,4. При n= 1 кривая становится равнобокой гиперболой.
|

