Техническое черчение

Диметрические прямоугольные проекции получаются на плоскости аксонометриче­ских проекций в том случае, если она накло­нена под одинаковыми углами не к трём главным направлениям, а только к двум. Обычно принимают такое положение плоскости проекций, при котором одинаковые искажения получатся по направлениям длины и высоты проектируемого предмета. Искажение по направлению глубины в этом случае получается вдвое большим, чем по направлению длины и высоты, и равно 0,47 натуральной величины. Коэффициент искажения по направлению длины и высоты равен 0,94. Практически коэффициенты искажения для прямоугольной диметрии принимают 1:0,5:1 и соответствующий им масштаб изображения 1,06:1.

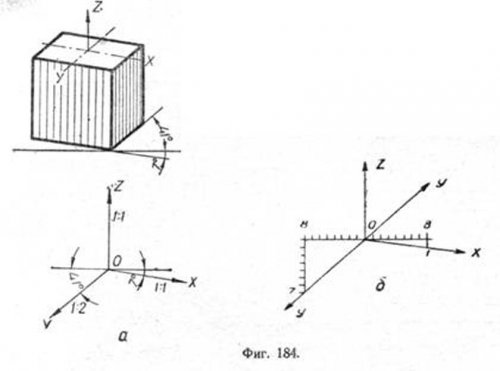
Проекции координатных осей X и Y будут наклонены к горизонтальной прямой, первая на 7° и вторая на 41° (фиг. 184,а). Построение этих же осей можно выполнить упрощённо (фиг. 184,б). Они определяются построением уклонов 1:8 для оси X и 7:8 для оси Y, соответствующим углам 7 и 41°.

Если плоскость аксонометрического проектирования параллельна какой-нибудь грани прямоугольного координатного трёхгранного угла, то при косоугольном проектировании два главных направления изобразятся в натуральную величину. При проектировании на плоскость P, параллельную XOZ, все прямые, параллельные этой плоскости, 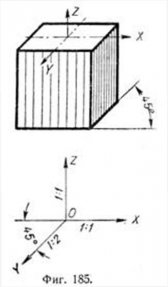изобразятся в натуральную величину. Поэтому изображением оси OZ является вертикальная, а оси ОX — горизонтальная прямые. Направление проектирования предполагается таким, при котором ось OY пересекает ОХ под углом 45° (фиг. 185).

Коэффициенты искажения равны единице для осей X и Z и 0,5 для оси Y.

Рассмотрим несколько примеров на построение прямоугольной диметрии для многогранных поверхностей.

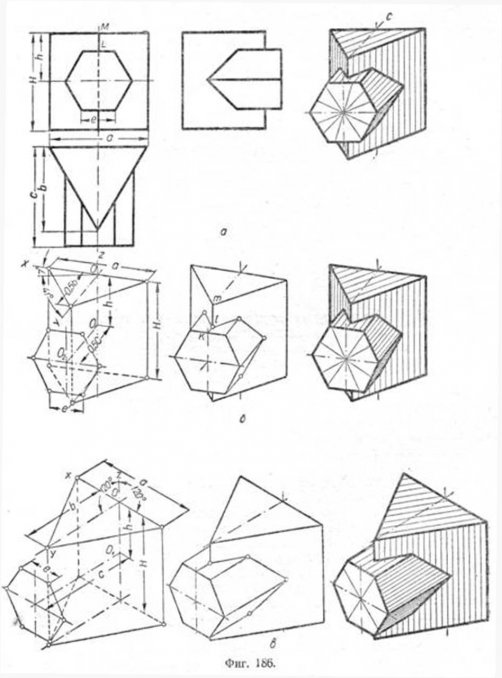
П p и м e р. Пусть требуется построить проекции двух пересекающихся призм по их ортогональным проекциям (фиг. 186) Проведём оси ОХ и OY под углами 7 и 41° к горизонтальной прямой. По оси ОХ, симметрично относительно точки О, отложим отрезок, равный а, a по оси ОY отрезок, равный b/2. Соединив конечные точки отрезков, получим верхнее основание треугольной призмы.

Отложив вниз по направлению OZ отрезок, равный H, построим нижнее основание той же призмы. Построение треугольной призмы заканчивается построением её боковых рёбер. Шесть вершин основания второй призмы строим по координатам. Для построения центра основания 0₂ построена ломаная О, О₁, 0₂, у которой OO₁=h и O₁O₂=0.5C.

Через точку О₂ проводим две прямые, параллельные осям ОХ и OZ, по которым откладываем в натуральную величину координаты каждой из вершин шестиугольника.

Точка эта легко определяется пересече­нием прямых kl || OY и lm || OO₁.

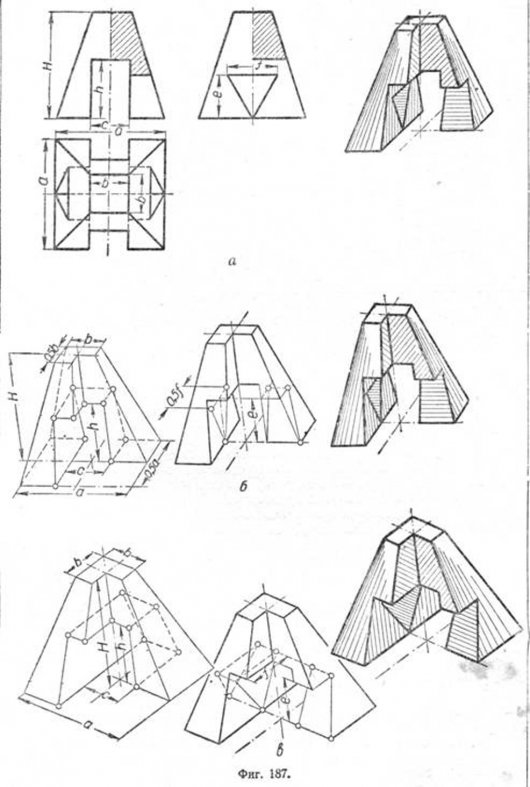
Для построения изометрической проекции тех же тел необходимо дать аксонометрическим осям направление, соответствующее указанному на фиг. 186,в, и принять для масштаба 1:1 коэффициент искажения 0,82:0,82:0,82, а для масштаба 1,22:1 коэффициент 1:1:1. На фиг. 187 даны построе­ния аксонометрических изображений по ортогональным проекциям для усечённой пирамиды с четырёхугольным основанием, пронизанной двумя другими призмами с треугольным и прямоугольным основаниями. Построения выполнены по этапам для изометрической и диметрической проекций аналогично построению на фиг. 186.

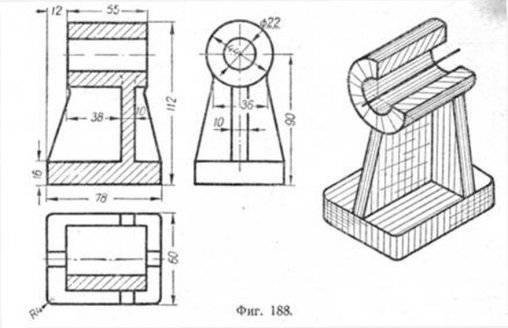
На фиг. 188 дан пример построения изометрической проекции для технической детали—стойки. Это построение выполнено по ортогональным проекциям.