Техническое черчение

Для передачи вращательного движения овала одного катка к другому необходимо, чтобы между поверхностями цилиндров существовало достаточное трение. Такая передача носит название фрикционной. Однако при больших нагрузках в такой передаче возможны проскальзывания одной цилиндрической поверхности по другой. Для того чтобы избежать проскальзывания и обеспечить постоянство передаточного отношения, поверхности цилиндров снабжают зубцами определённого профиля. Цилиндры с та­кими зубцами носят название цилиндрических зубчатых колёс (фиг. 316). Цилиндрические зубчатые колёса делятся на прямозубые, косозубые, шевронные и винтовые.

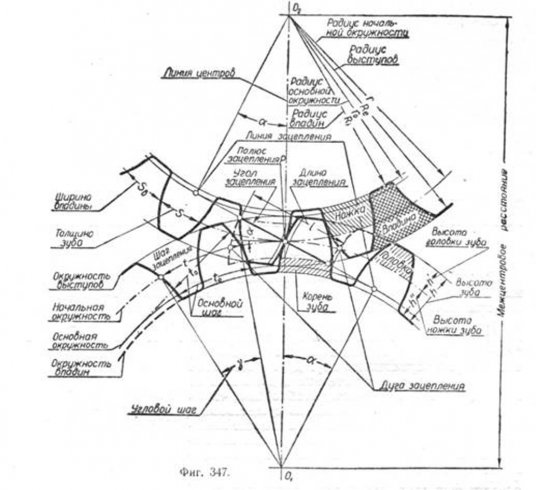
Основные обозначения по OCT/BKC 8089, относящиеся к зубчатым зацеплениям цилиндрических колёс, приведены на фиг. 347.

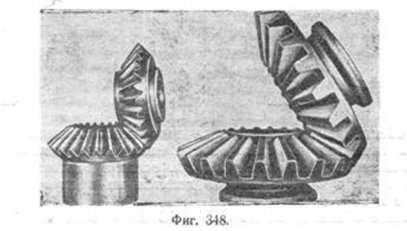
Если коническую поверхность снабдить зубцами, то получим кони­ческое зубчатое колесо (фиг. 348). Как и цилиндрические, конические колёса изготовляются с прямыми, косыми, криволинейными и шеврон­ными зубцами.

Таким образом, зубчатая передача отличается от фрикционной тем, что в ней ведущее и ведомое кол?са имеют той или иной формы зубцы,

которые, находясь в зацеплении между собой, передают вращение от ведущего вала к ведомому. Помимо привед?нных зубчатых передач (фиг. 346 и 348) в машиностроении также широко применяются червячные передачи, в которых передача вращательного движения осуществляется посредством червяка (винта), находящегося в зацеплении с цилиндрическим червячным коле­сом (фиг. 349).

Передача между параллельными валами осуществляется цилиндри­ческими зубчатыми колёсами; при пересекающихся валах применяются конические колёса. Передача между скрещивающимися валами осуще­ствляется винтовыми колёсами или червячной парой.

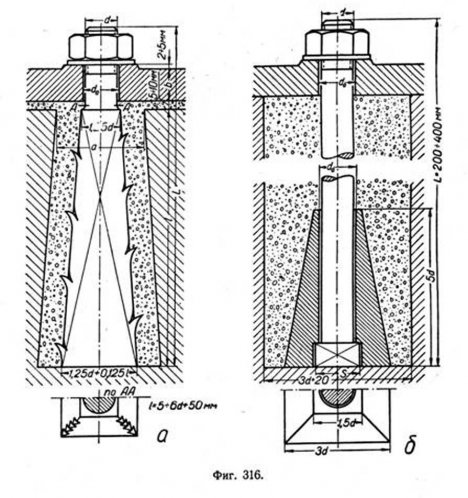
Цилиндрические зубчатые ко­лёса. Вычерчивание цилиндриче­ских зубчатых колёс производится по ГОСТ 3460-46. Зубцы колёс вы­черчиваются тремя условными ок­ружностями (фиг. 347): окружно­стью выступов, впадин и начальной окружностью.

Окружность выступов D_e вы­черчивается сплошной контурной линией, проходящей по кромкам выступов зубцов; окружность впа­дин D_i — штриховой линией, про­ходящей по основанию зубцов; на­чальная окружность d — штрих- пунктирной линией, являющейся делительной окружностью при по­строении профиля зубца.

Начальная окружность проходит между окружностями выступов и впадин и делит зубец по высоте на две части. Верхнюю часть h₁ назы­вают головкой зубца, а нижнюю h₂—ножкой. Таким образом, полная высота зубца h=h₁+h₂ (фиг. 347).

Размер зубца s по начальной окружности называют толщиной зубца, а расстояние s_в, измеренное по дуге начальной окружности,—шириной впадины. Сумму s + s_в=t называют шагом зацепления. В зубчатых зацеплениях зависимость между шагом t, числом зубцов z и диаметром начальной окружности d выражают формулой

d=t/? z.

Отношение шага t к числу ? называется модулем зацеплений, т. е. t/?=m, и тогда предыдущая формула примет вид

d = tnz.

Отсюда модуль можно выразить как отношение диаметра начальной окружности d к числу зубцов z, т. е. d/z = т. Модуль является основ­ным параметром зубчатых зацеплений. Высоту головки и ножки зубца выражают также через модуль. В прямозубых колёсах чаще всего при­нимают следующие соотношения: h₁ = m; h₂ = 1,2 m. В косозубых й шевронных колёсах часто принимают h₁=0,8 m.

Модули зубчатых передач стандартизованы. ОСТ 1597 устанавливает следующие модули: 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 1; 1,25; 1,5; 1,75; 2; 2,25; 2,5; (2,75); 3; (3,25); 3,5; (3,75); 4; (4,25); 4,5; 5; 5,5; 6; 6,5; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 18; 20; 22; 24; 26; 28; 30; 33; 36; 39; 42; 45; 50; последующие через 5 мм.

П p и м e ч а н и е. Модули, взятые в скобки, по возможности не применять.

На практике, при составлении чертежа с натуры, измерение диаметра начальной окружности d представляет некоторую трудность, поэтому определение его производится измерением диаметра выступов зубцов D_e.

Зная наружный диаметр (выступов), можно определить диаметр начальной окружности по уравнению

D_e =d + 2h₁

Принимая d = mz и h₁ = m, получим D_e = mz + 2m = m (z + 2), откуда определится модуль т. По модулю и числу зубцов находится d.

Диаметр окружности впадин D_i определится из уравнения

D_i = d—2h₂ = m (z—2,4)

или

D_i = D_e - 2h = m (z-4,4).

Следовательно, для вычерчивания зубчатого колеса необходимо знать лишь размеры: d, D_e, D_i . Остальными конструктивными размерами t, s, m пользуются при вычерчивании профиля зубцов, шаблонов для проверки шага зацепления и вдругих случаях. Так как все эти величины могут быть выражены через число зубцов и модуль, то для вычерчива­ния зубчатого колеса необходимо иметь две величины: число зубцов z и модуль m.

Пусть для примера даны: z=12 и m = 15. Требуется определить d, D_e, D_i .

Пользуясь приведёнными выше формулами, определяем: d= mz = 15 • 12=180 мм;

D_e = m(z+ 2) = 15(12 + 2) =210 мм;

D_i = De —2 • 2,2 m = 210 - 2 • 2,2 - 15 - 144 мм.

При вычерчивании зубчатого колеcа с натуры необходимо измерить диаметр окружности D_e и посчитать число зубцов. Остальные элементы зубцов определяются по формулам.

Пусть измеренный диаметр D_e =252 мм, число зубцов z= 16, тогда

m=D_e/(z+2) = 252/(1602)= 14 мм;

d = mz = 14 • 16 = 224 мм;

D_i = D_e —2 - 2,2 m = 252-2 - 2,2 • 14 = 190,4 мм или D_i = d - 2,4 m = 224—2,4 • 14 = 190,4 мм.

При вычерчивании зубчатого зацепления необходимо, чтобы началь­ные окружности имели точку касания на линии центров зубчатых колёс. Между окружностями выступов и впадин остаётся радиальный зазор, равный 0,2 т. Зубцы, попавшие в разрез, вычерчиваются нерассечёдными. На фиг. 350, 351 и 352 приведены изображения цилиндрических зубчатых колёс с простановкой размеров (размерны милиниями) и с необходимыми конструктивными и технологическими надписями.