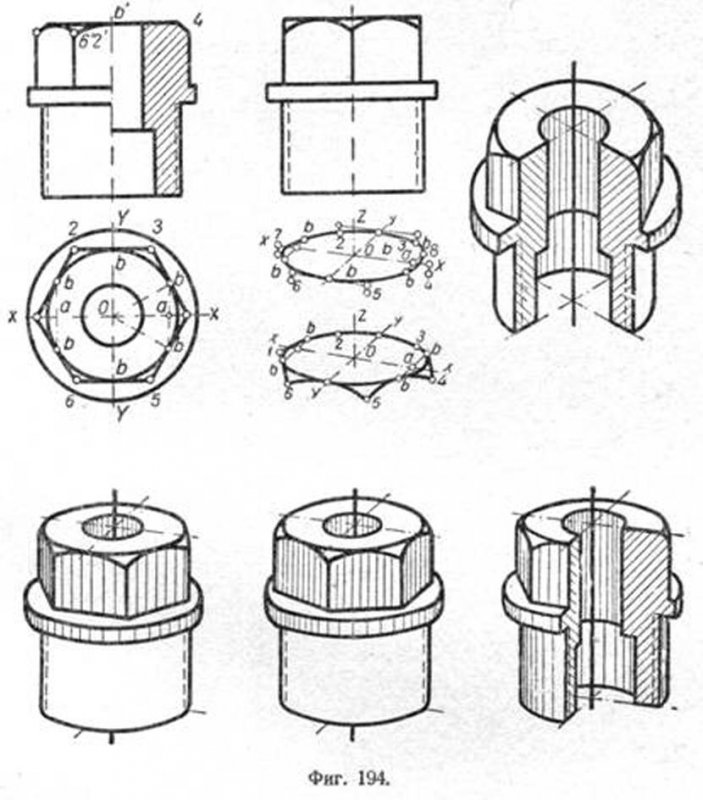
Торцы головки болтов, гаек, ниппелей имеют форму круга. Построение аксонометрической проекции окружности нам уже известно. Из чертежа видно, что кривые граней шестигранника касаются вписанной
в него окружности в точках b.
Построение точек b, через которые проходит ось Y, не требует пояснения. Для построения таких же точек на других гранях проведём на плане в прямоугольной проекции через эти точки перпендикуляры к оси X. Получим координаты этих точек: x=Oa и y=ab. Так как в диметрической проекции размеры по оси X не искажаются, то отрезок Oa, отложенный из центра О вправо и влево, изобразится неиска- жённым. Через полученные таким образом точки а проведём прямые, параллельные оси Y, и на них отметим от оси X в обе стороны отрезок, равный ab/2. Так определятся точки b. Далее строим нижние точки кривых 1, 6, 5, 4, 3 и 2. Для этого через точки касания b, лежащие на оси Y, проведём прямые, параллельные оси X, и на них отложим в натуральную величину ширину граней 6—5 и 2—3, а по оси X — отрезки 04 и 01 (точки 7 и 8). Через полученные точки проведём вниз вертикальные прямые и на них отложим отрезок, равный превышению точки касания b над точками 1, 6, 5 и т. д. Для этого измеряем по перпендикуляру на вертикальной проекции расстояние, например между 6' и торцевой частью ниппеля, и откладываем его соответственно в аксонометрической проекции. Полученные таким образом точки 1, 2, 3, 4, 5 и 6 соединяем по лекалу. Из чертежа видно, что не все кривые попали в поле зрения, часть их оказалась невидимой. Рядом показаны изображения ниппеля в изометрии и диметрии. Они выполнены с разрезами и без разрезов.
Образцы аксонометрических изображений деталей в косоугольной диметрии, прямоугольной диметрии и в изометрии приведены на фиг. 195, 196, 197, 198 и 199.
На фиг. 195 показан в трёх проекциях и в косоугольной диметрии корпус питательного клапана; на фиг. 196 — прямоугольная диметрия крышки карбюратора; на фиг. 197 — изометрия высоковольтного изолятора; на фиг. 198 и 199 — косоугольная диметрия центробежного насоса и изометрия редуктора.
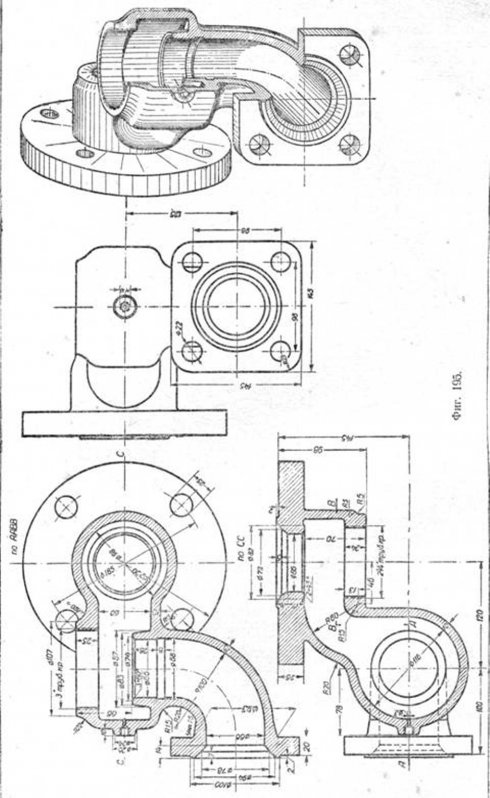
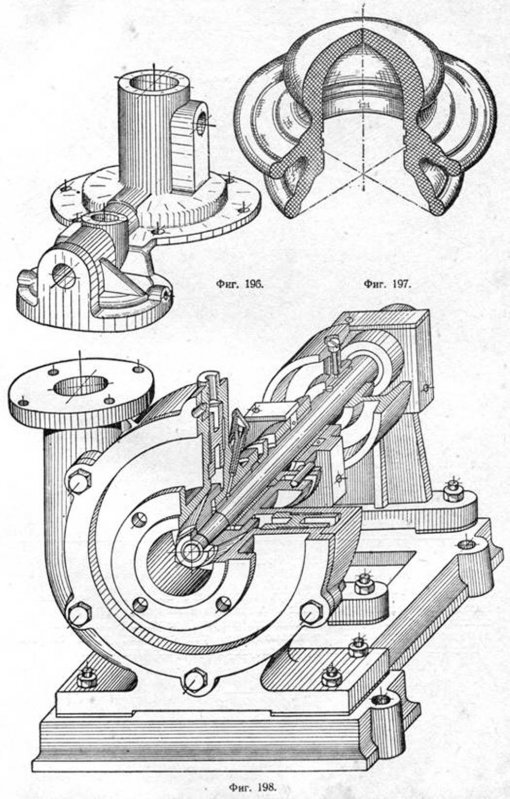
Следует заметить, что при построении сборочных чертежей в аксонометрических проекциях с разрезами валы, оси, штифты, болты, винты и т. п., попавшие в плоскости разреза, рекомендуется показывать в нерассечённом виде, за исключением тех случаев, когда секущая плоскость пересекает эти детали перпендикулярно к их осям.
]]>Каждый из этих эллипсов является проекцией окружности сечения поверхности шара плоскостью, параллельной одной из трёх координатных плоскостей.
Диаметр обёртывающей окружности равен диаметру шара.
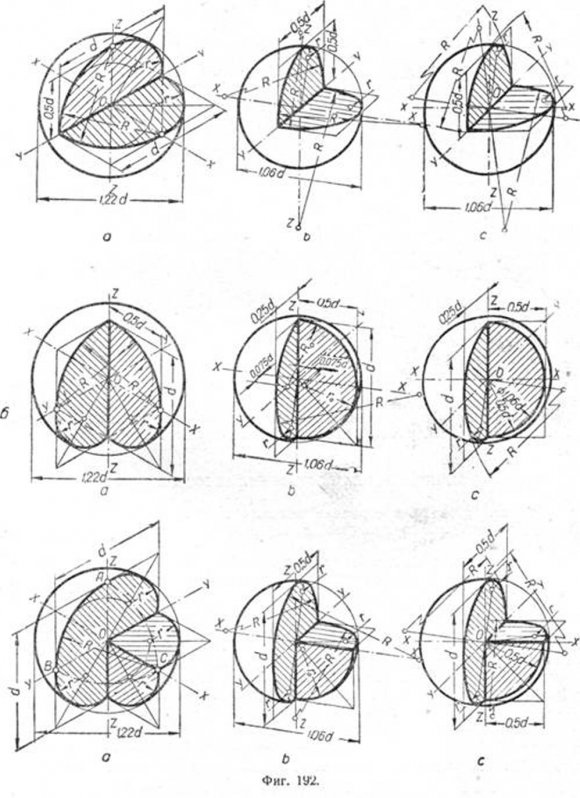
На фиг. 192 приведено построение сечений шара плоскостями в: а—изометрической, b —диметрической и c —косоугольной проекциях.
В приведённых примерах секущие плоскости совпадают с осями XOY и ZOY, XOZ и YOZ.
На фиг. 193 даны проекции пересечения шара с призмой, имеющей прямоугольное основание, и построение прямоугольной диметрии.
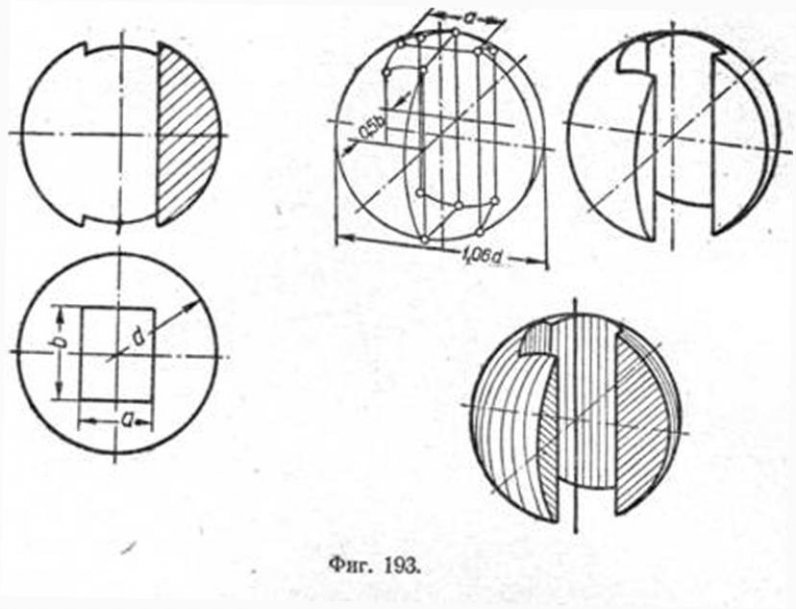
Построение линий пересечения призмы с шаром выполнено нахождением отдельных точек кривых пересечения. Этот способ следует предпочесть и для случаев, когда грани призмы пересекаются с шаром по плоскостям, не параллельным плоскостям проекций.
]]>Построим изометрическую проекцию окружности, лежащей в какой- нибудь координатной плоскости. Для этого возьмём куб, в грани которого впишем окружности. Куб расположим так, чтобы его грани были параллельны координатным плоскостям (фиг. 189).
Проекция куба имеет форму правильного шестиугольника, а проекцией каждой его грани является ромб.
Равенство ромбов—проекций квадратов—предопределяет и равенство эллипсов—проекций, вписанных в грани куба окружностей. Направления главных осей эллипса в изометрических проекциях совпадают с диагоналями ромба, в который вписан эллипс.
Следует запомнить простое правило нахождения большой и малой осей: малая ось всегда параллельна той оси, которой нет в названии плоскости эллипса. Так, например, если для эллипса плоскости OXZ нет названия оси OY, то малая ось этого эллипса параллельна оси OY. Большая ось всегда перпендикулярна к малой.
Можно это же условие выразить иначе: малая ось эллипса совпадает по направлению либо параллельна перпендикуляру к плоскости, в которой лежит спроектированная в эллипс окружность.
Чтобы построить эллипс по главным его осям, кроме направления, необходимы и размеры этих осей.
Как известно, независимо от положения плоскости проекций, большая ось эллипса всегда равна величине диаметра окружности, а малая в изометрической проекции равна 0,58 диаметра окружности. Приближённо можно принять отношение между осями эллипса, равным 3:5.
Если построение окружности выполняется в масштабе 1,22:1, то при построении большой оси надо взять 1,22 d, а для малой 3/5 этой величины, т. е. 0,725 d.
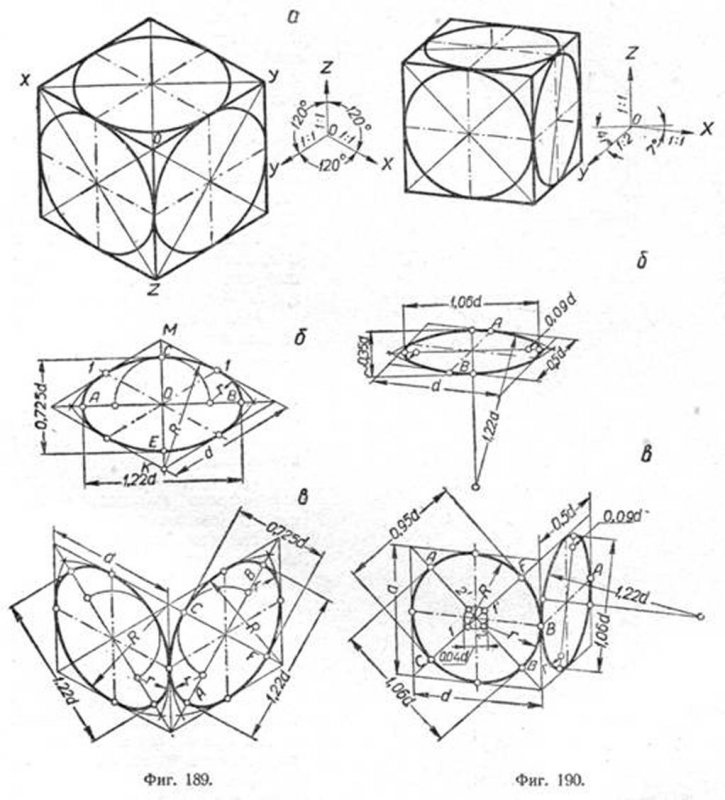
В практике часто вместо построения эллипсов лекальные кривые заменяют циркульными и строят овал с тем же отношением 3:5 между главными осями.
На фиг. 189,б и в приведён способ построения овалов, заменяющих вписанные эллипсы. На одном чертеже овал вписан в ромб, соответствующий горизонтальной грани куба, а на втором—двум боковым граням.
На фиг. 190 дана диметрическая прямоугольная проекция окружности. Свойства, перечисленные в предыдущем случае, остаются в силе и здесь.
Эллипс, в который проектируется окружность, лежащая на передней грани куба, имеет, как и в случае изометрических проекций, главные оси, сливающиеся с диагоналями куба. Конечные точки осей могут быть определены как точки, делящие каждую из полудиагоналей ромба на части в отношении 7:10.
Для боковой грани и для грани верхнего основания куба направление малой оси эллипса параллельно аксонометрической оси OY. Зная направление малых осей эллипсов, легко определить направление больших осей.
Для боковой грани большая ось наклонена к оси OZ на угол 7°, а для грани верхнего основания большая ось будет горизонтальной прямой.
При проектировании в масштабе 1,06:1 длина большой оси эллипса равна 1,06 d, где d — диаметр окружности.
Что касается малой оси, то для фронтальной грани она равна 0,89, т. е. около 0,9 большой оси. Для граней боковой и горизонтальной малая ось принимается равной 0,35 ребра куба или 1/3 большой оси эллипса.
Практически в этом случае вместо эллипсов можно строить овалы.
На фиг. 190, б и в показаны способы построения овалов для каждой грани отдельно.
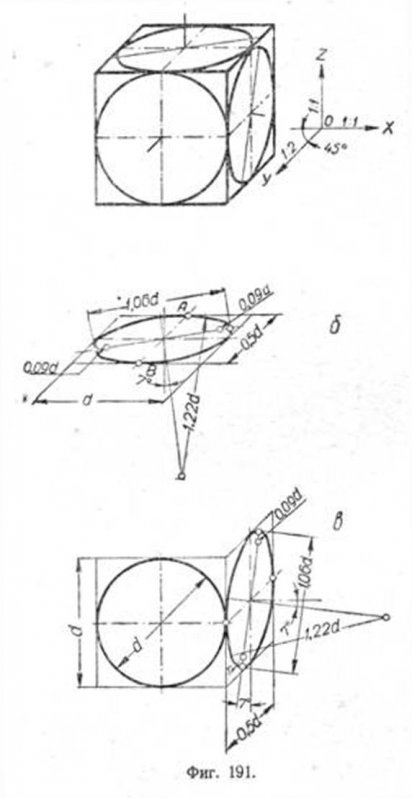
И, наконец, при косоугольном проектировании диметрическая проекция фронтальной грани куба проектируется без искажений; очевидно, и окружность, вписанная в эту грань, проектируется в окружность (фиг. 191, а и в).
Боковая грань и грань верхнего основания куба почти не отличаются по форме от соответствующих граней, построенных в прямоугольной проекции.
Овалы в этом случае вычерчиваются почти так же, как и на соответственных гранях куба предыдущего случая.
]]>Проекции координатных осей X и Y будут наклонены к горизонтальной прямой, первая на 7° и вторая на 41° (фиг. 184,а). Построение этих же осей можно выполнить упрощённо (фиг. 184,б). Они определяются построением уклонов 1:8 для оси X и 7:8 для оси Y, соответствующим углам 7 и 41°.
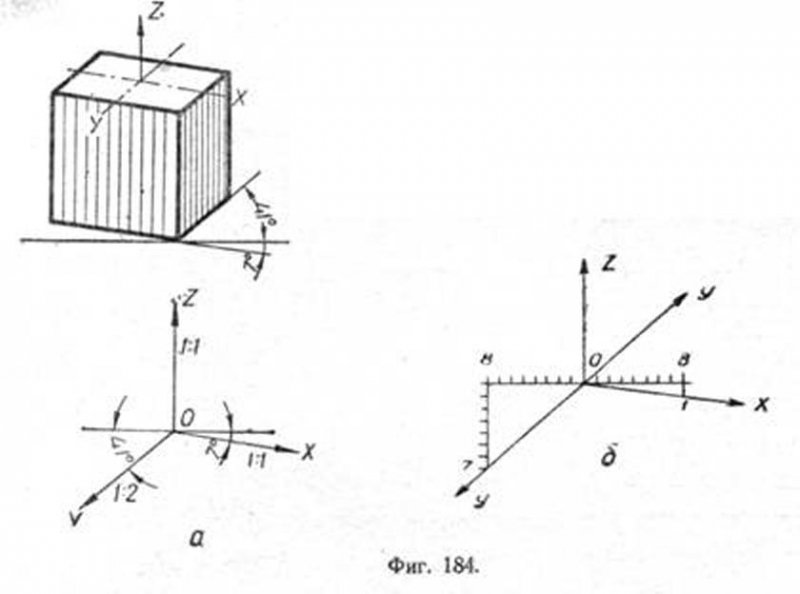
Если плоскость аксонометрического проектирования параллельна какой-нибудь грани прямоугольного координатного трёхгранного угла, то при косоугольном проектировании два главных направления изобразятся в натуральную величину. При проектировании на плоскость P, параллельную XOZ, все прямые, параллельные этой плоскости,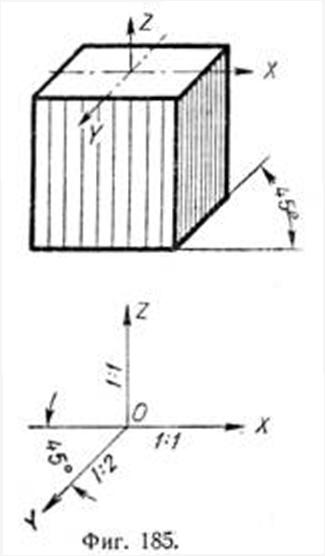 
изобразятся в натуральную величину. Поэтому изображением оси OZ является вертикальная, а оси ОX — горизонтальная прямые. Направление проектирования предполагается таким, при котором ось OY пересекает ОХ под углом 45° (фиг. 185).
Коэффициенты искажения равны единице для осей X и Z и 0,5 для оси Y.
Рассмотрим несколько примеров на построение прямоугольной диметрии для многогранных поверхностей.
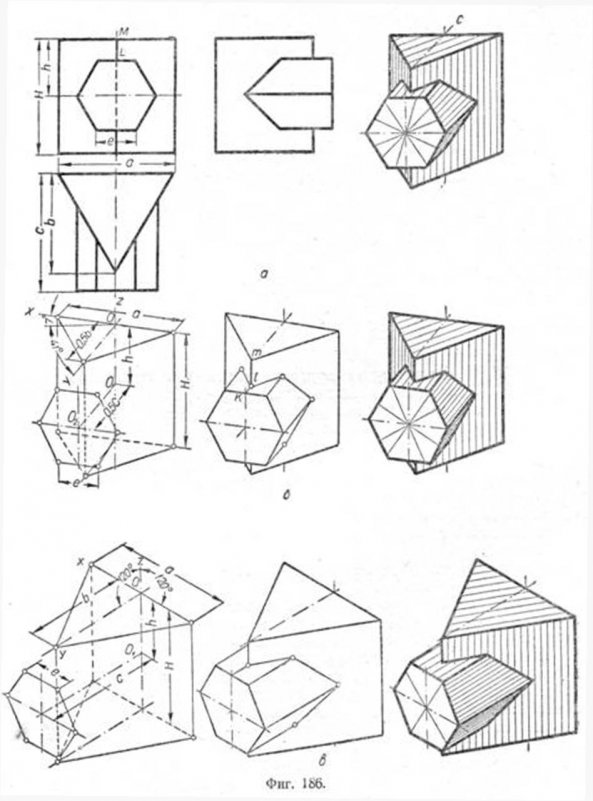
П p и м e р. Пусть требуется построить проекции двух пересекающихся призм по их ортогональным проекциям (фиг. 186) Проведём оси ОХ и OY под углами 7 и 41° к горизонтальной прямой. По оси ОХ, симметрично относительно точки О, отложим отрезок, равный а, a по оси ОY отрезок, равный b/2. Соединив конечные точки отрезков, получим верхнее основание треугольной призмы.
Отложив вниз по направлению OZ отрезок, равный H, построим нижнее основание той же призмы. Построение треугольной призмы заканчивается построением её боковых рёбер. Шесть вершин основания второй призмы строим по координатам. Для построения центра основания 02 построена ломаная О, О1, 02, у которой OO1=h и O1O2=0.5C.
Через точку О2 проводим две прямые, параллельные осям ОХ и OZ, по которым откладываем в натуральную величину координаты каждой из вершин шестиугольника.
Точка эта легко определяется пересечением прямых kl || OY и lm || OO1.
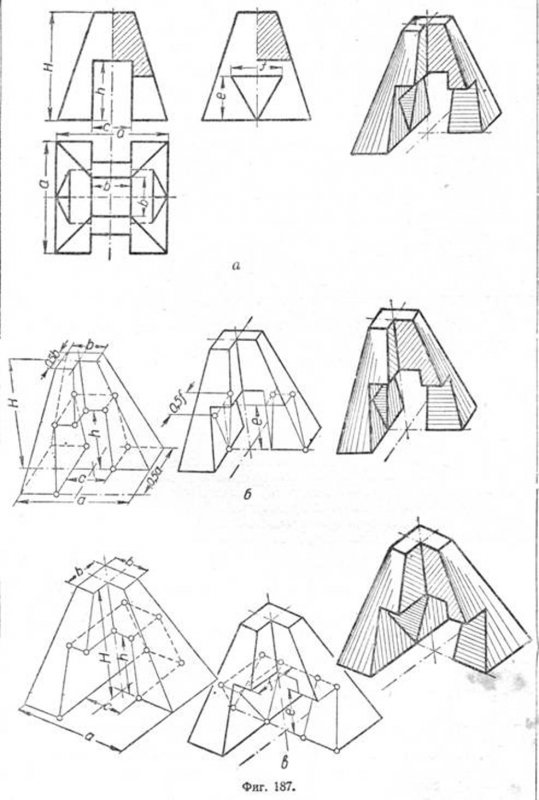
Для построения изометрической проекции тех же тел необходимо дать аксонометрическим осям направление, соответствующее указанному на фиг. 186,в, и принять для масштаба 1:1 коэффициент искажения 0,82:0,82:0,82, а для масштаба 1,22:1 коэффициент 1:1:1. На фиг. 187 даны построения аксонометрических изображений по ортогональным проекциям для усечённой пирамиды с четырёхугольным основанием, пронизанной двумя другими призмами с треугольным и прямоугольным основаниями. Построения выполнены по этапам для изометрической и диметрической проекций аналогично построению на фиг. 186.
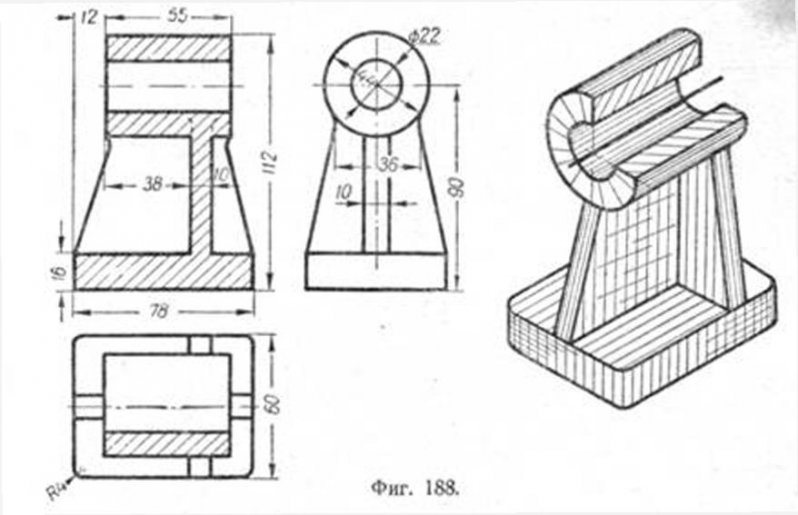
На фиг. 188 дан пример построения изометрической проекции для технической детали—стойки. Это построение выполнено по ортогональным проекциям.
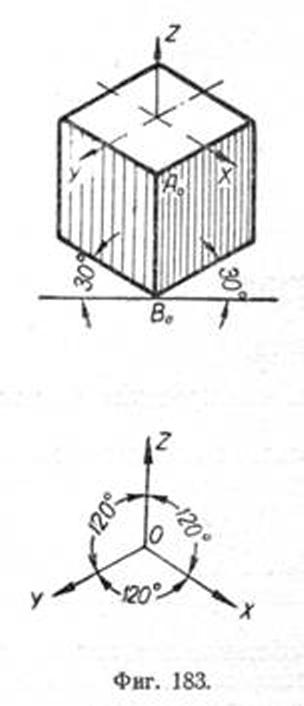Прямоугольная изометрическая проекция получается путём ортогонального проектирования предмета на аксонометрическую плоскость, наклонённую к координатным осям пространства, а следовательно, к главным направлениям длины, глубины и высоты под одинаковыми углами. Такая плоскость образует прямоугольный координатный трёхгранный угол по равностороннему треугольнику. Проекция начала координатных осей находится в центре этого треугольника, а аксонометрические оси OX, OY и OZ являются его высотами, пересекающимися между собой под углами в 120° (фиг. 183). Отрезок, равный натуральной единице длины, отложенный по любой из координатных осей, либо по направлению, параллельному этим осям, проектируется с искажением натуральной величины в 0,82 раза. Число 0,82 называется изометрическим показателем искажения. Если вместо коэффициента 0,82 принять коэффициент 1, что гораздо проще, то изображение построится правильным, но с линейным увеличением в 1/0.82 = 1,22 раза.]]>Аксонометрическое проектирование даёт наглядное изображение, понятное даже мало подготовленному лицу, поэтому при изготовлении чертежей, наряду с изображением в ортогональных проекциях, иногда прибегают к аксонометрическим изображениям. Кроме того, к аксонометрии прибегают при необходимости наиболее наглядно пояснить форму сложной детали лицам, не в достаточной степени владеющим методом ортогональных проекций.
Навыки, приобретаемые в упражнениях по составлению аксонометрических проекций способствуют развитию у учащихся способности пространственного представления, что значительно облегчает усвоение специальных дисциплин, как, например: теоретической и прикладной механики, деталей машин и др.
В черчении применяются два способа параллельного проектирования:
- Прямоугольное проектирование на плоскость, параллельную какой- нибудь паре главных направлений, например, на плоскость, параллельную направлению длины и высоты проектируемого предмета. Такие проекции называются ортогональными.
- Прямоугольное проектирование на плоскость, не параллельную какой-либо паре главных направлений, называемое аксонометрическим. Частным случаем аксонометрических проекций являются косоугольные проекции на плоскость, параллельную какой-нибудь паре главных направлений.
Легко убедиться в том, что если проектируемый предмет, например куб, поставить в положение, удобное для построения ортогональных проекций, и спроектировать его на плоскость аксонометрических проекций, то при удачном выборе угла наклона последней аксонометрическое изображение получится более наглядным, чем ортогональное.
В черчении применяются изометрические и диметрические проекции.
]]>